Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 74

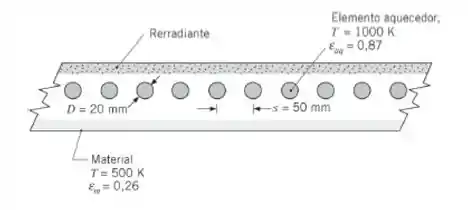
Um aquecedor radiante é constituído por um banco de tubos cerâmicos com elementos aquecedores internos. Os tubos têm diâmetro D = 20 mm e estão separados por uma distância s = 50 mm. Uma superfície rerradiante está posicionada por trás dos tubos de aquecimento como mostrado na figura. Determine o fluxo térmico radiante líquido para o material aquecido

quando os tubos de aquecimento (εaq = 0,87) são mantidos a 1000 K. O material aquecido (εm = 0,26) está a uma temperatura de 500 K.

Passo 1

Vamos lá!! Queremos saber o fluxo térmico que chega no material!!

Mas antes de qualquer coisa, vamos definir como superfície 1 os elementos aquecedores, superfície 2 o material aquecido e R a superfície rerradiante!!

q 2 ' ' !! Uma das superfícies é rerradiante, ou seja, isolada, dessa forma podemos usar:

q 2 = σ ( T 2 4 - T 1 4 ) 1 - ε 1 ε 1 A 1 + 1 A 2 F 2 1 + 1 A 1 F 1 R + 1 A 2 F 2 R - 1 + 1 - ε 2 ε 2 A 2

Como queremos q 2 ' ' podemos dividir q 2 por A 2 :

q 2 = A 2 σ ( T 2 4 - T 1 4 ) 1 - ε 1 ε 1 A 1 + 1 A 2 F 2 1 + 1 A 1 F 1 R + 1 A 2 F 2 R - 1 + 1 - ε 2 ε 2 A 2

Passo 2

Da tabela 13.1 tiramos a expressão pro fator de forma F 21 :

F 21 = 1 - 1 - D s 2 1 2 + D s tan - 1 ⁡ s 2 - D 2 D 2    

Lembrando que:

D = 20   m m

s = 50   m m

Não precisa converter, afinal F 2 1 é adimensional:

F 2 1 = 1 - 1 - 20 5 0 2 1 2 + 20 50 tan - 1 ⁡ 50 2 - 20 2 2 0 2 = 0 , 5472  

A gente ainda precisa de F 1 R e F 2 R , pela regra da simetria:

F 21 = F R 1

Pela regra da soma:

F R 2 = 1 - F R 1 = 1 - 0,5472 = 0,4528

Pela regra da reciprocidade:

A 1 F 1 R = A R F R 1

A 2 F 2 R = A R F R 2

Passo 3

Sabendo que:

A 1 = π D L = π × 0,020 L

A 2 = A R = s L = 0,05 L

Podemos achar q 2 ' ' :

q 2 ' ' = A 2 σ ( T 2 4 - T 1 4 ) 1 - ε 1 ε 1 A 1 + 1 A 2 F 21 + 1 A R F R 1 + 1 A R F R 2 - 1 + 1 - ε 2 ε 2 A 2

Substituindo:

q 2 = 0,05 L × 5,67 × 10 - 8 × ( 500 4 - 1000 4 ) 1 - 0,87 0,87 × 0,020 × π L + 1 0,05 L × 0,5472 + 1 0,05 L × 0,5472 + 1 0,05 L × 0,4528 - 1 + 1 - 0,26 0,26 × 0,05 L

Podemos cortar L e calcular:

q 2 = - 12,590   W / m 2

Aweeee!!!

Resposta

q 2 = - 12,590   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Revestimentos aplicados a longas tiras metálicas são curados pela instalação das tiras ao longo das paredes de um longo forno com seção transversal quadrada.As condições térmicas no interior do forno
O revestimento sobre uma superfície metálica com dimensões de 1 m por 2m é curado pela sua colocação sob uma superfície eletricamente aquecida de dimensões equivalentes, a uma distância de 0,5 m. O co
Barras longas e cilíndricas são termicamente tratadas em um forno infravermelho. As barras, com diâmetro D = 50 mm, são colocadas sobre uma bandeja isolada e são aquecidas por um painel infravermelho
A base de um gerador de vapor de água com 200 mm de diâmetro é aquecido por radiação. O aquecedor, mantido a 1000°C e separado do gerador por uma dist��ncia de 100 mm, tem o mesmo diâmetro da base do
Um longo elemento aquecedor cilíndrico, com diâmetro D = 10 mm, temperatura T1 = 1500 K e emissividade ε1 = 1, é utilizado em um forno. A área da base do forno A2 é uma superfície cinza e difusa, com