Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 63
Um fluido criogênico escoa por um tubo com 20 mm de diâmetro, cuja superfície externa é difusa e cinza, com uma emissividade de 0,02 e uma temperatura de 77 K. Esse tubo é concêntrico a um tubo maior, com 50 mm de diâmetro, cuja superfície interna é difusa e cinza, com uma emissividade de 0,05 e uma temperatura de 300 K. Há vácuo no espaço entre as superfícies. Determine o calor ganho pelo fluido criogênico, por unidade de comprimento do tubo interno. Se uma barreira de radiação com parede delgada, difusa e cinza, com emissividade de 0,02 (os dois lados), for inserida no meio da distância entre as superfícies interna e externa, calcule a variação (percentual) no ganho de calor, por unidade de comprimento do tubo interno.
Passo 1
Vamos lá!! O Temos duas situações, na primeira não temos barreira e na segunda temos!
O enunciado é bem direto, ele quer saber quanto de calor chega no fluido criogênico por unidade de comprimento, ou seja na superfície do tubo interno!, para as duas situações e depois a gente variação no ganho de calor!
Vamos pegar tudo que o enunciado disse e fazer um esqueminha:
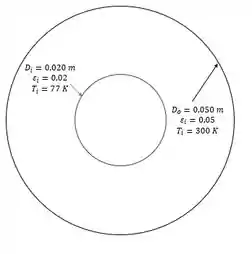
Montando um esqueminha das resistências, temos:
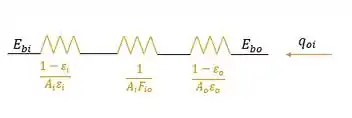
Escrevendo, ficamos com:
O calor que chega no tubo interno é o calor que sai do tubo externo, certo?
Mas a gente quer o calor por unidade de comprimento:
Passo 2
Vamos colocar a mão na massa então:
Substituindo :
Mas , como é igual pra todo mundo, então podemos isolar ele:
Cortando o :
Se e :
Achamos o calor ganho pelo fluido criogênico:
Passo 3
Agora vamos fazer a mesma coisa, só que dessa vez tem uma barreira entre os tubos:
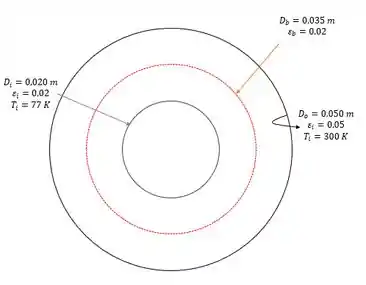
Vamos montar a resistência já cortando o , beleza?
Escrevendo, ficamos com:
Podemos calcular
Substituindo:
Calculando:
Passo 4
Agora só falta calcular a variação em porcentagem!!!
Para isso fazemos:
Substituindo:
Uhuuuuul!!!