Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 59
Transferência de calor por radiação ocorre entre duas grandes placas paralelas, que são mantidas a temperaturas T1 e T2, com T1 > T2. Para reduzir a taxa de transferência de calor entre as placas, propõe-se que elas sejam separadas por uma barreira delgada que tenha emissividades diferentes em suas superfícies opostas. Em particular, uma superfície tem a
emissividade εb,
- Como a barreira deve ser orientada para proporcionar a maior redução na taxa de transferência de calor entre as placas? Isto é, a superfície com emissividade εb ou a com emissividade 2εb deve estar orientada na direção da placa com temperatura T1?
- Que orientação irá resultar no maior valor da temperatura da barreira Tb?
Passo 1
Vamos lá! Temos duas placas grandes paralelas entre si com uma barreira entre elas, mas não sabemos ainda qual é a emissividade das superfícies da barreira, portanto temos duas situações possíveis:
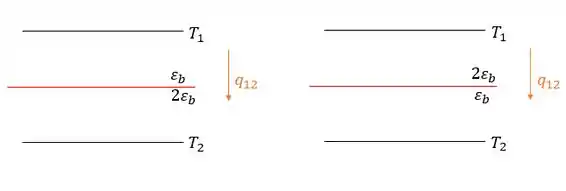
A letra a quer saber em qual das duas opções a barreira vai ser mais efetiva, em qual o valor de vai ser menor, vamos montar um esqueminha das resistências radiantes e espaciais:
Esse esqueminha representa a primeira configuração das placas, somando as resistências temos:
Para a segunda configuração, a gente tem que trocar as resistências do meio de lugar, mas como a resistência total é a soma de todas as resistências, logo independente da configuração a resistência será a mesma!
Passo 2
Agora queremos saber qual configuração vai resultar na maior temperatura da barreira, ! Para isso vamos considerar a taxa de transferência entre a placa superior e a barreira,
Nesse caso a resistência desse circuito pode ser escrita:
Repara que apareceu ali no final um , que pode ser:
Ou:
E o que queremos é exatamente descobrir qual vai resultar na maior !
Se, , podemos então escrever :
O termo representa uma diferença de potêncial e é proporcional a diferença de temperatura entre as duas superfícies, então, quanto maior for o valor de , maior vai ser a temperatura da barreira!
Vamos isolar :
Quanto menor o valor de , maior vai ser o valor de e maior a ! Agora, qual retorna pra a gente a menor valor?
Isso mesmo!!
Que corresponde ao segundo caso!!
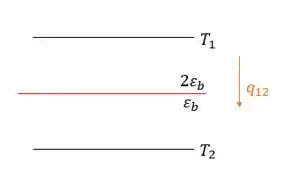
Uhuuuul!!
Resposta
- A taxa de transferência de calor idepende da disposição da barreira.
- No segundo caso.