Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 15
15. No exemplo 9-18 resolvemos a equação de Navier-Stokes para escoamento laminar permanente, completamente desenvolvido em um tubo redondo (escoamento de Poiseuille), desprezando a influencia da gravidade. Agora, acrescente novamente o efeito da gravidade resolvendo novamente esse mesmo problema, mas use a pressão modificada em lugar da pressão real . Especificamente, calcule o campo real de pressão e o campo de velocidade. Suponha que o tubo é horizontal e que o plano de referência esteja a alguma distância arbitrária abaixo do tubo. A pressão real no topo do tubo é maior, igual, ou menor do que aquela na base do tubo? Discuta.
Passo 1
O Calculo do campo de velocidade real pode ser obtido procedendo-se da seguinte forma beleza?
A equação de Navier stokes para um fluxo laminar totalmente desenvolvido e em um tubo redondo sem gravidade considerada é semelhante à equação de Navier stokes para um fluxo laminar totalmente desenvolvido em um tubo redondo com gravidade considerada. Como não há superfície livre no fluxo e, portanto, o termo gravidade não mostra nenhum efeito no campo de velocidade. Esse é todo o conteúdo derivado no exemplo 9-18 permanecerá o mesmo, exceto que a pressão real P que é substituída pela pressão modificada .
Portanto, o campo de velocidade real permanece o mesmo que foi resolvido no exemplo 9-18 da equação (9).
Aqui, u é a velocidade real do campo e R é o raio da haste cilíndrica infinita.
Portanto, o campo de velocidade real é .
Passo 2
Para se obter o campo de pressão modificado fazemos o seguinte:
A pressão real varia com , e a partir de um ponto começa a diminuir linearmente com , como no exemplo 9-18, neste caso de pressão modificada também é variável linearmente e diminui linearmente com.
Escrevendo a pressão modificada no local onde se torna ,
Aqui está a pressão modificada no local em que x se torna ,
Portanto, o campo de pressão modificado é .
Obtemos então, o campo de pressão real da seguinte maneira:
Antes de mais nada, devemos escrever a expressão para o campo de pressão hidrostática,
Aquela equaçãozinha clássica de Mec Fluidos!!
Para obter o valor da cabeça de pressão real, subtraia a equação da pressão modificada da equação da pressão hidrostática.
Portanto, a pressão real da cabeça P é .
Um esboço do tubo em questão utilizado no problema pode ser mostrado como:
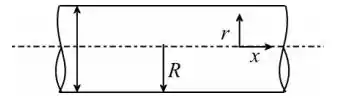
Passo 3
O tubo é um tubo horizontal longo e redondo, com a parte superior do tubo mais alta que a parte inferior do tubo,
A partir da equação da pressão hidrostática, é claro que a pressão e as cabeças de referência são inversamente proporcionais entre si,
Portanto, a pressão aumenta de cima para baixo à medida que flui para baixo.
Portanto, a pressão real no topo é menor que a pressão no fundo .