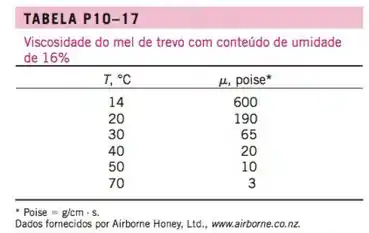
17. A viscosidade do mel de trevo está listada em função da temperatura na Tabela P10-17. A gravidade específica do mel é aproximadamente 1,42 e não é uma função que dependa fortemente da temperatura. O mel é pressionado através de um pequeno furo de diâmetro na tampa de uma jarra de mel virada para baixo. O ambiente e o mel estão à temperatura . Estime a velocidade máxima do mel através do furo, de maneira que o escoamento possa ser aproximado como escoamento lento. (Suponha que Re deve ser menos de 0,1 para que a aproximação do escoamento lento seja adequada.) Repita o seu cálculo se a temperatura for de 40°C. Discuta.

Encontramos a relação para a velocidade máxima do mel através do orifício da equação numérica de Reynolds.

Reorganizando a equação e escrevendo a fórmula da velocidade máxima do mel.

Obtemos a viscosidade dinâmica do mel de trevo na  tabela P10-20 (Viscosidade do mel de trevo com 16% de umidade) no livro.

Agora, utilizando o fator de conversão para converter as unidades de viscosidade dinâmica de equilíbrio para .

Convertendo as unidades teremos:

Utilizamos a relação obtida a partir da equação de Re para calcular a velocidade máxima do mel através do furo.

Portanto, a velocidade máxima do mel através do orifício em  é .

Temos que escrever a relação necessária para calcular a densidade do mel em .

Obteremos a densidade da água na  tabela do Apêndice A-3 (Propriedades da água saturada) no livro.

Então,

Obteremos a viscosidade dinâmica do mel de trevo na  tabela P10-20 (Viscosidade do mel de trevo com 16% de umidade) no livro.

Utilizando,então, o fator de conversão para converter as unidades de viscosidade dinâmica de equilíbrio para .

Convertendo as unidades teremos:

Utilizamos a relação obtida a partir da equação de Re para calcular a velocidade máxima do mel através do furo.

Portanto, a velocidade máxima do mel através do orifício em  é .

Uma temperatura maior, obtém um valor menor para a velocidade máxima.

Com isso, podemos concluir o que é muito mais fácil alcançar um passo lento para as menores temperaturas.

Contando uma vez que a viscosidade aumenta rapidamente com a diminuição da temperatura.