Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 20

Ar a 20°C e 1 atm escoa a 20 m/s em torno da placa plana da Figura P7.20. Um tubo de Pitot, colocado a 2 mm da parede, apresenta uma leitura manométrica h = 16 mm de óleo vermelho Meriam, d = 0,827. Use essa informação para determinar a posição x do tubo de Pitot a jusante. Considere escoamento laminar.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos ar a 20 ° C ( ρ = 1,2   k g / m ³ , μ =   1,8 × 10 - 5   P a ∙ s ) escoando em torno de uma placa plana a U = 20   m / s , como demonstra a figura que ilustra a questão.

Temos um tubo de Pitot posicionado em uma posição x desconhecida e a y = 2   m m da parede. Nas condições do escoamento, o manômetro apresenta uma leitura de h = 16   m m com o fluido manométrico sendo óleo vermelho Meriam ( d = 0,827 ).

A questão pede que a gente determine a posição x do tubo de Pitot. Pra isso, vamos assuir escoamento laminar e utilizar a solução exata de Blausius, dada pela Equação (7.2) dada na página 471.

u U = f ' ( η )

η = y U ν x 1 / 2

Sendo ν = μ ρ   a viscosidade cinemática

Agora vamo lá resolver essa questão juntos!

Passo 2

Em primeiro lugar, vamos calcular a velocidade do ar no ponto onde o tubo de Pitot está instalado:

u =   2 ρ o i l - ρ a r g h ρ a r = 2 827 k g m 3 - 1,2 k g m 3 9,81 m 2 s 0,016   m 1,2   k g / m ³

u = 14,7   m / s

Passo 3

Agora, vamos utilizar o resultado do passo anterior para calcular o valor de f ' ( η ) , a partir da equação:

f ' η =   u U = 14,7   m / s 20   m / s = 0,735

Agora, vamos calcular η utilizando a Tabela 7.1, dada na página 472. Vamos entrar com o valor de f ' ( η ) e encontrar esse valor:

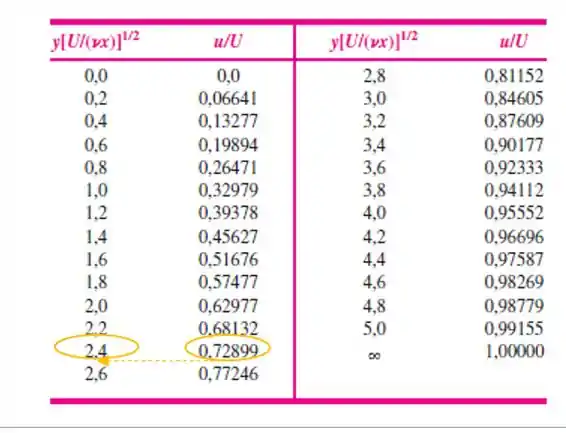
Portanto, η ≈ 2,4 .

Agora, podemos calcular o valor de x :

η = y U ν x 1 / 2 → 2,4 = 0,002   m 20   m / s 1,5 × 10 - 5 m 2 s x 1 / 2

x = 0,91   m

Passo 4

Por fim, devemos checar se o escoamento é realmente laminar como havíamos assumido.

Pra isso, vamos calcular o número de Reynolds:

R e x = ρ U x μ = 1,2 k g m 3 20 m s 0,91   m 1,8 × 10 - 5   P a ∙ s = 1,21 × 10 6

Que prova que o escoamento é laminar e que assumimos corretamente.

Pronto, matamos a questão juntos!

Resposta

A posição do tubo de Pitot a jusante é x = 0,91   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento sobre a placa divisora do Problema 9.38. Mostre algebricamente que a força de arrasto total sobre um lado da placa pode ser escrita como F D = ρ U 2 θ L b . Avalie θ L e o arras
O perfil de velocidade em um escoamento da camada limite laminar com gradiente de pressão zero é aproximado pela expressão linear dada no Problema 9.10. Use a equação da integral da quantidade de movi
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 5m / s , porém considerando que a base da placa está de fr
Usando os resultados numéricos obtidos por Blasius (Tabela 9.1), avalie a distribuição de tensão de cisalhamento em uma camada limite laminar sobre uma placa plana. Trace τ / τ w versus y / δ . Compar
Considere o escoamento de ar sobre uma placa plana. Em um gráfico, trace a espessura da camada limite laminar como uma função da distância ao longo da placa (até a transição), para velocidades de corr