Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 36
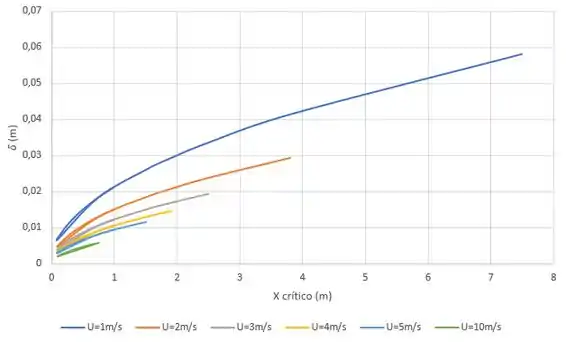
Considere o escoamento de ar sobre uma placa plana. Em um gráfico, trace a espessura da camada limite laminar como uma função da distância ao longo da placa (até a transição), para velocidades de corrente livre , , , , e .
Passo 1
A ideia aqui é esboçar a camada limite para o escoamento laminar para cada caso de velocidade de corrente livre. Lembrando que a partir de um valor de (distância ao longo da placa), não teremos mais o escoamento laminar, logo depois desse valor de x, para cada caso, a gente interrompe o gráfico nesse ponto.
Para esboçar esse gráfico, a gente vai precisar achar uma relação entre a expessura da camada limite e a distância ao longo da placa, para cada caso. Bora!
Passo 2
Podemos calcular primeiro o valor de , onde não teremos mais o escoamento laminar para cada caso.
Para fazer isso precisamos lembrar de duas coisinhas:
A primeira é a expressão para encontrar o valor de :
A segunda é lembrar qual é o crítico para o caso de uma placa laminar. Para esse caso, o escoamento vai ser laminar se:
Considerando , como viscosidade cinemática do ar a .
Para :
Fazendo essa mesma continha para as outras velocidades:
Passo 3
Temos essa equaçãozinha aqui que relaciona a expessura da camada linear ( com o valor da distância ao longo da placa (:
Sabendo que:
Podemos substituir uma na outra, jogar o para o outro lado e arrumar:
Achamos a relação entre e .
Passo 4
A partir dessa relação a gente pode plotar o gráfico para cada caso, lembrando de interromper o gráfico para cada . Por exemplo, para o caso , nosso gráfico é interrompido em .
Depois de calcular a expressão de cada caso, nossas camadas limites ficam assim:
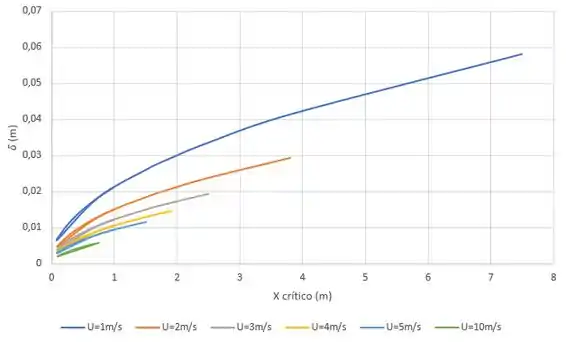
Resposta
