Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 21

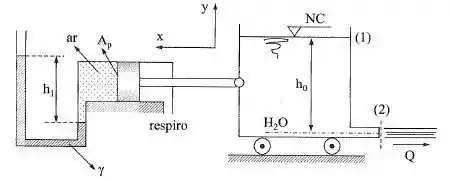
Sabendo que o sistema da figura encontra-se em equilíbrio, desprezando as perdas, determinar a altura . (; ; )

Passo 1

Vamos começar o exercício calculando a pressão no pistão, que pode ser encontrada com o auxílio do manômetro instalado nele, então, temos:

Agora vamos encontrar a força que o pistão exerce no sistema, sabemos que a força é o produto da área pela pressão, então:

Passo 2

Agora vamos aplicar a equação da força que o fluido exerce sobre um anteparo entre os pontos 1 e 2, então, a equação se torna:

Vamos calcular a equação na direção :

Podemos escrever a vazão mássica como:

Substituindo essa relação na equação para a força, temos:

Passo 3

Agora, sabemos que para o equilíbrio do sistema, o módulo das duas forças devem ser iguais, então, temos:

Substituindo os valores encontrados:

Agora para encontrar a altura do reservatório vamos aplicar o equilíbrio de cargas entre os pontos 0 e 2:

Substituindo os valores conhecidos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pequeno motor de foguete é utilizado para acionar um dispositivo a “jato portátil” destinado a elevar um só astronauta acima da superfície da Lua. O motor do foguete produz um jato uniforme com vel

O tanque móvel mostrado deve ser desacelerado pelo abaixamento de uma concha que capta água de um reservatório. A massa e a velocidade iniciais do tanque, com seu conteúdo, são m 0 e u 0 , respectivam

Deseja-se uma bomba que, acoplada a um motor de 3450 rpm, produza uma altura manométrica teórica de 80 m. O ângulo de entrada das pás deve ser de 15º e o de saída, de 30º. Sendo d 1 = 10c m , quanto d

Uma bomba centrífuga tem pás com ângulo de entrada 15º e de saída de 25º. A rotação é 1720 rpm e os diâmetros de entrada e saída são, respectivamente, de 10cm e 25cm. Sendo v u 1 = 0 e v r 1 = v r 2 ,

No dispositivo da figura, o pistão de peso G = 29,4k N desce muito lentamente dentro do cilindro de área 2m 2 , empurrando a água ( γ = 10 4N / m 3 ) pelos dois cotovelos instalados simetricamente. A