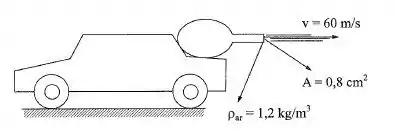
Um fabricante de brinquedos constrói um carrinho impulsionado pelo ar de uma bexiga. No instante inicial em que é liberado o ar, determinar:

a) a força de propulsão;

b) a pressão do ar da bexiga, desprezando a perda de carga e supondo o ar incompressível.

Vamos começar o exercício já aplicando a equação da força que o fluido exerce sobre um anteparo, no caso, teremos o ponto 1, que fica dentro da bexiga, e o ponto 2, logo na saída dela, então, a equação se torna:

Vamos calcular a equação na direção :

Podemos escrever a vazão mássica como:

Substituindo essa relação na equação para a força, temos:

Substituindo os valores conhecidos, temos: