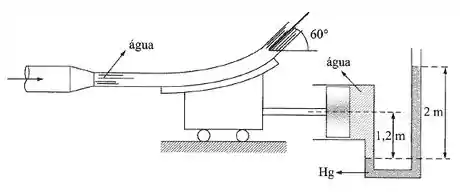
Dado o esquema da figura, sabendo que a seção do jato tem uma área de 520 cm² e que a área do pistão é 20 cm², determinar a vazão no bocal. Dados: ; . Observação: o sistema está em equilíbrio.

Agora vamos aplicar a equação para a força exercida pelo fluido sobre o anteparo, dada por:

Vamos aplicar a equação na direção :

No entanto, sabemos que as velocidades nos pontos 1 e 2 são iguais, já que a vazão é constante e o diâmetro do jato não se altera. E sabemos também que podemos escrever a vazão mássica como:

Então, substituindo essa expressão na equação para a força, temos:

Como o enunciado nos disse que o sistema está em equilíbrio, então sabemos que a força exercida pelo fluido é a mesma força exercida pelo pistão, então temos:

Substituindo os valores conhecidos, temos:

Agora podemos finalmente encontrar o valor da vazão volumétrica do sistema: