Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 2
Óleo de motor a e a uma velocidade de escoa sobre as duas superfícies de uma placa plana com de comprimento mantida a . Determine:
(a) As espessuras das camadas-limite de velocidade e térmica na aresta de saída da placa.
(b) O fluxo térmico local e a tensão de cisalhamento na superfície local na aresta de saída da placa.
(c) A força de arrasto e a taxa de transferência de calor totais, por unidade de largura da placa.
(d) Represente graficamente as espessuras das camadas-limite e os valores locais da tensão de cisalhamento na superfície, do coeficiente convectivo e do fluxo térmico como uma função de .
Passo 1
Temos óleo escoando com uma temperatura e velocidade sobre uma placa de comprimento e temperatura . O item (a) nos pede para determinar as espessuras das camadas limites térmica e de velocidade ao final da placa.
Para isso, vamos começar calculando a temperatura de filme. Ela é dada por:
Nesta temperatura as propriedades do óleo são (Tabela A-5, apêndice A):
O próximo passo é calcular o número de Reynolds para verificar se o escoamento é laminar ou turbulento. Ele é dado por:
Para escoamento paralelo à placa: representa um escoamento em regime laminar. A partir das propriedades do óleo podemos utilizar as relações de espessura de camada limite em regime laminar. Começando pela de velocidade:
Para a camada limite térmica:
Passo 2
Para o item (b) precisamos encontrar o fluxo térmico local ao fim da placa. Para isso, vamos começar calculando o coeficiente convectivo para escoamento paralelo a uma placa, em regime laminar:
A partir do coeficiente podemos calcular o fluxo de transferência de calor por convecção:
Ainda no item (b) devemos determinar a tensão de cisalhamento na aresta de saída da placa. Para isso, vamos aplicar a relação:
Passo 3
Para o item (c) devemos determinar a força de arrasto e a taxa de transferência de calor por convecção, por largura da placa.
Vamos começar relembrando que:
Para regime laminar:
Então:
Vamos agora para a taxa de convecção:
Para regime laminar:
Então:
Passo 4
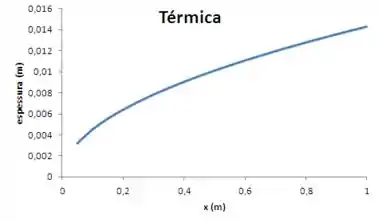
Vamos agora para o item (d). Devemos graficar as espessuras das camadas limites de velocidade e térmica, além do coeficiente convectivo, a tensão de cisalhamento e o fluxo térmico para vários valores de , dentro do comprimento da placa.
Como primeiro passo, vamos escrever todas essas propriedades em função de . Então:
E para espessura da camada limite térmica
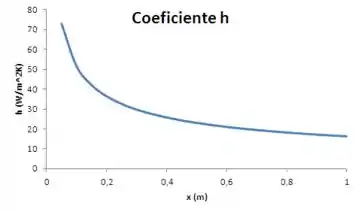
O próximo é o coeficiente convectivo local:
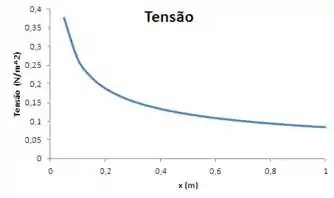
A tensão de cisalhamento local será:
Por fim, o fluxo de calor por convecção:
Com auxílio de Excel, ou outra ferramenta gráfica, podemos plotar o gráfico de cada uma dessas funções, para diversos valores de dentro do intervalo . Devemos obter algo da forma:
Resposta
(a)
.
(b)
.
(c)
.