Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 36
Ar, a 27°C e com uma velocidade na corrente livre de 10 m/s, é usado para resfriar componentes eletrônicos montados sobre uma placa de circuito impresso. Cada componente, com 4 mm x 4 mm, dissipada 40 mW, que são removidos pela superfície superior dos componentes. Um gerador de turbulência está localizado na aresta frontal da placa, fazendo com que a camada-limite seja toda turbulenta.
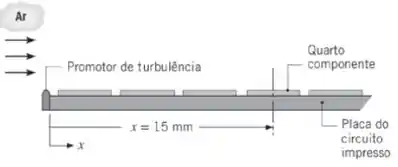
- Estime a temperatura da superfície do quarto componente, localizado a 15 mm da aresta frontal da placa.
- Gere um gráfico da temperatura da superfície dos quatro primeiros componentes como uma função de velocidade na corrente livre para .
- Qual é a velocidade mínima na corrente livre se a temperatura superficial do componente mais quente não pode ultrapassar 80 °C?
Passo 1
Precisamos estimar a temperatura no quarto componente. E ai? Como fazer???
Simples! Vamos assumir que todo o calor dissipado por cada componente é dissipado por convecção. Portanto, temos a seguinte relação:
Uma relação que conhecemos bastante né? Se isolarmos a temperatura da superfície , e substituirmos os valores de algumas constantes, temos:
E quem é o coeficiente ? Esta que é a grande dificuldade da letra a). Então, vamos trabalhar separadamente este termo.
Passo 2
Agora, vamos calcular o coeficiente de transferência de calor . Para isto, precisamos entender as condições que o componente está sujeito para podermos escolher a correlação correta para o número de Nusselt (e consequentemente, para o coeficiente).
A questão já nos disse que estamos trabalhando em escoamento turbulento. Esta é uma informação importante. A outra, que é o “pulo do gato”, é que nos vamos aproximar o coeficiente convectivo médio no componente pela relação de coeficiente pontual. Isto é,
Portanto,
Antes de seguirmos os cálculos com os números de Reynolds, precisamos determinar as propriedades do ar. E para isto, precisamos da temperatura da superfície (que é o que queremos determinar) para poder calcular a temperatura de filme.
Então, como não temos esta temperatura, vamos fazer um “chute” inicial. Supondo que , a temperatura de filme será . Se, ao final da questão, a nossa resposta estiver bem diferente, teremos que repetir todo o procedimento.
Então, com esta temperatura de filme e sabendo que o ar está a 1 atm, da tabela , temos: , , .
Continuando, vamos calcular o número de Reynolds. Então, temos:
Portanto, o coeficiente de transferência de calor será:
Então, a temperatura da superfície será: