Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 53

53. Ar, a 27°C e com uma velocidade de 5 m/s, passa sobre a pequena região As (20 mm × 20 mm) de uma grande superfície, que é mantida a Ts = 127°C. Nessas condições, uma taxa de 0,5 W é removida da superfície As. Com objetivo de aumentar a taxa de remoção de calor, um pino de aço inoxidável (AISI 304) com diâmetro de 5 mm é fixado sobre a superfície As

que supostamente permanece a Ts = 127°C.

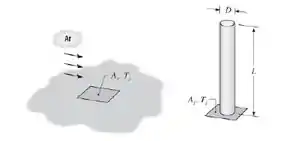
(a) Determine a taxa de remoção de calor máxima possível através do pino.

(b) Qual comprimento do pino propiciaria uma boa aproximação da taxa de transferência de calor determinada na parte (a)? Sugestão: Veja o Exemplo 3.9.

(c) Determine a efetividade do pino, εa.

(d) Qual é o aumento percentual na taxa de transferência de calor na superfície As causado pela instalação do pino?

Passo 1

Primeiro devemos Calcular a temperatura média do filme.

T f = T ∞ + T s 2

T f = 27 + 127 2

= 77 + 273

= 350 K

Obtenha as propriedades do ar na tabela A.4, “Propriedades termo-físicas dos gases à pressão atmosférica”, à temperatura  350 K .

A viscosidade cinemática é, v = 20,92 × 10 - 6 m 2 s  

O coeficiente de condutividade térmica é, k = 30,0 × 10 - 3 W m . K  

O número Prandtl é, P r = 0,700  

Obtenha a condutividade térmica ( k ) para aço inoxidável k a ç o = 15,8 W m . K  

Passo 2

Letra (a)

Calcule o número de Reynolds.

R e D = V D v

R e D = 5 × 5 m m × 10 - 3 m 1 m m 20,92 × 10 - 6

= 1195

Como o número de Reynolds é  R e < 2000 , o fluxo é laminar.

Calcule o número de Nusselt.

N u D = C R e D m P r a 1 3

h - D k = C R e D m P r a 1 3

h - = k D C R e D m P r a 1 3       ( 1 )

Obtenha o valor das constantes da tabela 7.2, “Constantes da equação para o cilindro circular em fluxo cruzado”, no número de Reynolds entre 40 - 4000 .

O valor de  C é, C = 0,683

O valor de  m é, m = 0,466

h - = 30,0 × 10 - 3 5 m m × 10 - 3 m 1 m m 0,683 × 1195 0,466 0,700 1 3    

= 98,85   W m 2 . K

Calcule a máxima transferência de calor.

q f = h - P k A c 0,5 θ b       ( 2 )

= h - k π D π 4 D 2 0,5 T s - T ∞

= h - k D D 2 0,5 π T s - T ∞

= 98,85 π × 5 m m × 10 - 3 m 1 m m 15,8 π 4 0,005 2 0,5 127 - 27

= 2,194   W

Portanto, a taxa máxima de transferência de calor possível através da aleta é  2,194   W .

Passo 3

Letra (b)

Calcule o comprimento da aleta.

L ∞ = 2,65 k A c h - P 0,5

L ∞ = 0,0374   m

Portanto, o comprimento da barbatana é  0,0374   m .

Passo 4

Letra (c)

Calcule a eficácia.

ε f = q f h S A c , b θ b

ε f = q f q W o A S θ b A c , b θ b

ε f = 89,39

Aqui,  q W 0 o calor é removido da superfície.

Portanto, a eficácia é  89,39 % .

Passo 5

Letra (d)

Calcule a remoção geral de calor.

q W = q f + h s A s - A c , b T s - T ∞

= 2,194 + 0,4755

= 2,67   W

Calcule o aumento percentual na taxa de calor  A s   devido à instalação da aleta.

% I = q W - q W 0 q W 0 × 100

% I = 2,67 - 0,5 0,5 × 100

= 434 %

Portanto, o aumento percentual na transferência de calor é  434 % .

Resposta

  1. 2,194   W
  2. L ∞ = 0,0374   m
  3. ε f = 89,39
  4. 434 %
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

55. Seja o fio de níquel cromo (D = 1 mm, ρe = 10−6 Ω · m, k = 25 W/(m · K), ε = 0,20) usado para fabricar o aquecedor de ar do Problema 3.86, mas agora sob condições nas quais o coeficiente de transf
O objetivo de um experimento executado por estudantes é o de determinar o efeito da presença de pinos (aletas piniformes) na resistência térmica entre uma placa plana e uma corrente de ar. Uma placa q
Considere o processo de pulverização de plasma discutido nos Problemas 5.25 e 7.82. Para um diâmetro de saída do bocal de D = 10 mm e um raio do substrato de r = 25 mm, estime a taxa de transferência
Uma sonda criogênica é usada para tratar tecido cutâneo canceroso. A sonda é constituída por um único jato circular de diâmetro Dsai = 2 mm emanado de um bocal encapsulado concentricamente no interior