Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 61
61. Considere o uso do sensor de filme quente descrito no Problema 7.60 para determinar a velocidade da água entrando no sistema de resfriamento de uma planta de potência elétrica, oriunda de um lago próximo. O sensor é montado no interior de um tubo de alimentação e o seu controle é especificado para manter uma temperatura do filme quente média 5°C maior do que a temperatura do fluido (Ts,fq – T∞ = 5°C).
(a) Se uma medida independente da temperatura da água fornece um valor de T∞ = 17°C, use a correlação de Churchill–Bernstein para estimar a velocidade da água sob condições nas quais a alimentação de potência do sensor mantém um fluxo térmico de q″fq = 4 × 104 W/m2 do filme para a água.
(b) Se o sensor for exposto a água por um período extenso, sua superfície será suja pela acumulação de depósitos trazidos pela água. Considere condições nas quais os depósitos formam uma cobertura com 0,1 mm de espessura ao redor do sensor e têm uma condutividade térmica de kd = 2 W/(m · K). Para T∞ = 17°C e a velocidade do escoamento
determinada na parte (a), qual fluxo térmico tem que ser fornecido ao sensor para manter a sua temperatura em Ts,fq = 22°C? Qual é o erro correspondente na medida da velocidade? Nota: A condução através dos depósitos pode ser aproximada como aquela através de uma
parede plana.
Passo 1
Letra (a)
Calcule a temperatura do filme do ar atmosférico.
Obtenha as propriedades da água na tabela A.6 (Propriedades termo-físicas da água saturada) à temperatura :
O valor da viscosidade da água na temperatura usando a interpolação entre os valores de temperatura e :
O valor da viscosidade da água na temperatura usando a interpolação entre os valores de temperatura e :
.
O valor da viscosidade da água na temperatura usando a interpolação entre os valores de temperatura e :
Calcule a densidade da água à temperatura :
Calcular a viscosidade cinemática da água.
Calcule o número médio de Nusselt.
Ao substituir os valores obtemos:
Calcule o número de Reynolds.
Escreva a relação entre o fluxo de calor e o coeficiente médio de transferência de calor .
Escreva a relação entre o número médio de Nusselt e o coeficiente médio de transferência de calor por convecção.
Portanto, a velocidade da água é .
Passo 2
Letra (b)
Desenhe o circuito térmico do sensor de filme quente depois que os depósitos formarem uma casca grossa.
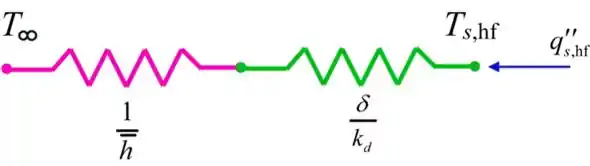
Calcule o número de Reynolds.
Calcule o número médio de Nusselt.
Ao substituir os valores obtemos:
Calcule o coeficiente médio de transferência de calor por convecção.
Calcular o fluxo de calor deve ser fornecido ao sensor para manter sua temperatura em .
Escreva a relação entre o fluxo de calor e o coeficiente médio de transferência de calor .
Escreva a relação entre o número médio de Nusselt e o coeficiente médio de transferência de calor por convecção.
Calcule o erro correspondente na medição de velocidade.
Portanto, o erro correspondente na medição de velocidade é .
Resposta
b)