38 - Por questões de saúde, espaços públicos requerem a substituição contínua de uma certa massa de ar interno viciado por ar externo fresco. Para conservar energia durante a estação de aquecimento, é comum recuperar a energia térmica do ar interno aquecido que é descartado e transferi-la para o ar externo frio que é alimentado no ambiente interno. Um trocador de calor de escoamento cruzado acoplado com os dois fluidos não misturados é instalado nos dutos de alimentação e descarga de um sistema de aquecimento como mostrado no esquema. Água, contendo um agente anticongelante é usada como fluido de trabalho no trocador de calor acoplado, que é composto por dois trocadores de calor A e B. Deste modo, calor é transferido do ar quente viciado para o ar frio fresco através da água que é bombeada através dos trocadores A e B.

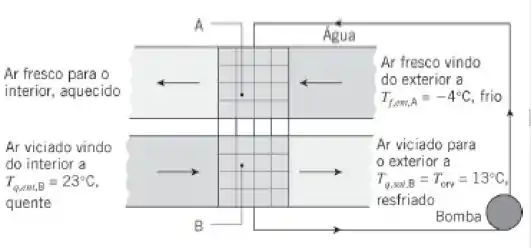
Sejam uma vazão mássica de ar especificada (em cada duto) de , um produto área–coeficiente global de transferência de calor de (para cada trocador de calor), uma temperatura do lado externo de e uma temperatura do ambiente interno de . Como o ar quente foi umidificado, uma transferência de calor excessiva pode resultar em condensação nos dutos, fato não desejado. Qual vazão mássica de água é necessária para maximizar a transferência de calor e garantir uma temperatura de saída associada ao trocador B não inferior a temperatura de orvalho, ? Sugestão: Suponha que a taxa de capacidade calorífica máxima está associada ao ar.

Vamos tomar as propriedades na média entre a temperatura externa e a temperatura interna, usando a seguinte relação.

Aqui  é a temperatura ambiente interno e   é a temperatura do lado externo.

Agora precisaremos obter alguns valores que são tabelados para prosseguir na resolução, tais valores são encontrados na tabela A.6 (Propriedades termo físicas da água saturada) e na A.4(Propriedades termo físicas do ar).

Nesse caso precisaremos realizar uma interpolação entre e , para obter as propriedades à temperatura de :

O calor específico da água é:

O calor específico do ar é:

Agora, venha comigo para calcular a capacidade máxima de aquecimento usando a seguinte fórmula:

Aqui  é a vazão mássica do ar e o  calor específico do ar.

Agora que temos a capacidade máxima, já conseguimos calcular a taxa de transferência de calor usando a seguinte fórmula:

Aqui, é a temperatura de saída associada ao trocador B

Como já temos todos as variáveis, basta substituirmos na equação.

Temos que o NTU (número de unidades de transferência) é usado para calcular a taxa de transferência térmica em trocadores de calor. Em termos de coeficiente geral de transferência de calor é dado por,

Aqui,  é o coeficiente geral de transferência de calor vezes a área. Como temos o valor de , podemos substitui-lo.

A taxa de transferência de calor real pode ser determinada de imediato pela expressão 11.22.

Igualando as equações (5) e equação (6), obtemos a seguinte relação:

Vamos utilizar a seguinte equação para calcular a eficácia:

Para encontrar a relação da capacidade térmica temos a seguinte relação:

Por tentativa e erro, obtemos:

Vamos agora encontrar a vazão de água usando a seguinte fórmula:

Assim, a vazão da água que é necessária para maximizar a transferência de calor, garantindo que o trocador de calor B não caia abaixo da temperatura do ponto de orvalho é .