42 - Vapor de água saturado a é condensado em um trocador de calor casco e tubos (1 passe no casco; 2, 4, … passes nos tubos) com um valor de de . A água de resfriamento entra a .
(a) Calcule a vazão de água de resfriamento requerida para manter uma taxa de transferência de calor de .
(b) Supondo que seja independente da vazão, calcule e represente graficamente a vazão da água requerida para fornecer taxas de transferência de calor na faixa de a . Comente sobre a validade de suas suposições.
Passo 1
Imagine o trocador de calor da seguinte forma:
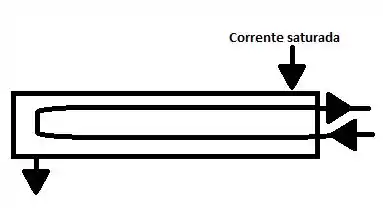
Precisamos de algumas premissas para resolver o problema:
- Condições de estado estacionário.
- Não há perda de calor para o ambiente.
- As propriedades se mantem constantes.
Passo 2
Antes de prosseguirmos, iremos ter que obter o calor específico da água a . Tal dado, pode ser obtido na tabela A.6
O Calor específico é:
Temos que o NTU (número de unidades de transferência) é usado para calcular a taxa de transferência térmica em trocadores de calor. Fornecido por meio da seguinte equação:
E por:
Aqui, é o coeficiente global de transferência de calor, é a área do tubo.
Onde:
Se observamos, temos no problema um vapor de água saturada e água. Nesse caso, temos que o fluido quente é saturada, logo , dessa forma .
Passo 3
Temos que a eficácia é a razão entre a taxa real de transferência de calor e a taxa máxima de transferência de calor, como mostrado abaixo:
A taxa máxima de transferência de calor pode ser determinada de imediato pela expressão seguinte expressão.
Aqui, é a temperatura de entrada do fluido quente e é a temperatura de saída do fluido frio.
Agora, venha comigo para obtermos uma nova equação por meio da substituição da na equação , assumindo .
Vamos agora obter a última equação, por meio da substituição da equação na , obtendo a seguinte fórmula:
Sabemos que , logo:
Temos por último, que , dessa forma temos:
Passo 4
Agora, basta substituirmos os valores na equação .
Como podemos observar temos a variável dos dois lados, por isso não conseguimos resolver de forma manual. Por isso temos que usar o software IHT para achar a vazão de água. O valor obtido será:
Portanto, a vazão de água de resfriamento requerida para manter uma taxa de transferência de calor de é .
Resposta
a).
b)É necessário o uso de software .