39 - Um trocador de calor de escoamento cruzado, usado em um procedimento de bypass cardiopulmonar, resfria sangue escoando a uma vazão de de uma temperatura do corpo de a para induzir a hipotermia do corpo, que reduz o metabolismo e as exigências oxigênio. O refrigerante é água gelada a 0°C e sua vazão é ajustada para fornecer uma temperatura de saída de . O trocador de calor opera com os dois fluidos não misturados e o coeficiente global de transferência de calor é igual a . A massa específica e o calor específico do sangue são e , respectivamente.
(a) Determine a taxa de transferência de calor no trocador.
(b) Calcule a vazão da água.
(c) Qual é a área da superfície do trocador de calor?
(d) Calcule e represente graficamente as temperaturas de saída do sangue e da água como uma função da vazão da água na faixa de a , supondo que todos os outros parâmetros permaneçam inalterados. Comente sobre como as variações nas temperaturas de saída são afetadas pelas variações na vazão da água. Explique esse comportamento e por que ele é uma vantagem para esta aplicação.
Passo 1
Considere os estados de entrada e saída do trocador de calor.
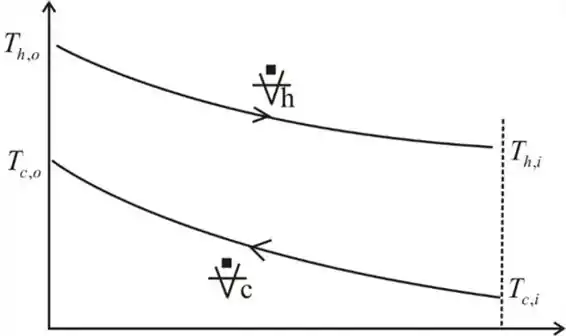
.
Passo 2
a) Vamos aplicar o balanço energético no trocador de calor, o calor perdido pelo fluido quente (sangue) deve ser igual ao calor ganho pelo fluido frio.
Podemos então encontrar a vazão mássica do fluido quente (sangue) da seguinte maneira.
Aqui é a densidade do fluido e é a taxa de fluxo volumétrico do sangue.
Passo 3
Vamos agora calcular a capacidade de calor do fluido quente.
Portanto o calor removido do sangue é dado por:
Dessa forma, a taxa de transferência de calor para o trocador de calor é .
Passo 4
b) Antes de prosseguirmos, precisamos calcular a temperatura de filme para fluido frio.
Agora precisaremos obter alguns valores que são tabelados para prosseguir na resolução, tais valores são encontrados na tabela A.6 (Propriedades termo físicas da água saturada).
O calor específico de fluido frio é:
A densidade do fluido frio é:
Passo 5
Temos que a taxa de transferência de calor é dada por:
Agora que temos a vazão do fluido, podemos encontrar a vazão do volume de fluido frio (água).
Portanto, a taxa de fluxo de fluido frio é .
Passo 6
c) A taxa de transferência de calor usando a diferença de temperatura média do log é escrita como:
A diferença de temperatura média do log para um trocador de calor de fluxo cruzado é expressa como:
aqui, é a diferença de temperatura média do log do trocador de calor de contra fluxo e é o fator de correção.
Temos que:
Substituindo as temperaturas de operação do trocador de calor na relação acima, obtemos:
Passo 7
O fator de correção é avaliado a partir da figura 11.12 usando os parâmetros e .
Os parâmetros e para um trocador de calor de fluxo cruzado com ambos os fluidos não misturados são:
Ao substituir as temperaturas operacionais do trocador de calor nas relações acima,
Passo 8
Com e temos que o fator de correção da figura 11.12 é . Logo:
Agora que temos todas as variáveis, podemos encontrar a área desejada voltando na transferência de calor.
Portanto, a área de superfície do trocador de calor de fluxo cruzado é .
Resposta
- É necessário o uso de software (IHT).