Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 135

Vapor saturado de água condensa a 100°C no lado do casco de um trocador de calor de 1 passe no casco e dois 2 passes no tubo com área de superfície de 0,5 m² e um coeficiente global de transferência de calor total de 2000 W m 2 K . A água fria c p c = 4179 J k g K que flui a 0,5 k g s entra no tubo lateral a 15°C. Determine a temperatura de saída da água fria e a taxa de transferência de calor do trocador de calor.

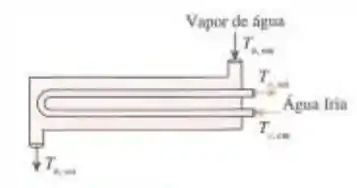
Passo 1

Bora continuar !!

Vamos começar achando a taxa de transferência de calor do trocador, tudo bem?

E para isso vamos usar a relação:

Q ˙ = ε Q ˙ m a x

Vamos lembrar que:

Q m a x ˙ = C m i n T q ,   e n t r a - T f ,   e n t r a

Se:

T q ,   e n t r a = 100 ° C

T f ,   e n t r a = 15 ° C

Mas nós ainda precisamos achar C m i n , certo?

Para achar os valores de C nós precisamos lembrar que:

C = m ˙ c p

Então:

C q = m v ˙ c p , v

C f = m a ˙ c p , a

Vamos ver nossos dados?

c p , a = 4 1 79 J k g K

m a ˙ = 0,5 k g s

Como nós não temos nenhuma informação sofre o vapor vamos assumir que:

C m i n = C f = 0,5 k g s 4179 J k g K = 2089,5 W K

Colocando no calor máximo:

Q m a x ˙ = 2089,5 W K 100 ° C - 15 ° C

Q m a x ˙ = 177,6   k W

Ainda precisamos da efetividade, não é?

Passo 2

Bom galerinha, no caso de um condensador a efetividade é dada por:

ε = 1 - e - N T U

Ixiiii!!

Não temos o NTU, mas sabemos que:

N T U = U A s C m i n

Se:

U = 2000 W m 2 K

A s = 0,5   m ²

C m i n = 2089,5 W K

Então:

N T U = 2000 W m 2 K 0,5   m ² 2089,5 W K = 0,4785

Substituindo na efetividade:

ε = 1 - e - 0,4785

ε = 0,38

Com a efetividade e a transferência de calor máxima podemos calcular a taxa real:

Q ˙ = 0,38 × 177,6   k W

Q ˙ = 67,488   k W

Leegal, já achamos uma das respostas!

Bora pra segunda?

Passo 3

Como já temos quanto calor é transferido podemos usar a relação abaixo e achar a temperatura de saída do fluido frio, a água:

Q ˙ = C f T f ,   s a i - T f ,   e n t r a

Sabendo que:

Q ˙ = 67,488   k W

T f ,   e n t r a = 15 ° C

C f = 2 , 0895 k W K

Então:

67,488   k W = 2 , 0895 k W K T f ,   s a i - 15 ° C

T f ,   s a i = 47,298 ° C

E finalizamos mais umaaaa !!

Resposta

Q ˙ = 67,488   k W       |       T f ,   s a i = 47,298 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

43 - Um trocador de calor casco e tubos (1 passe no casco, 2 passes nos tubos) deve ser usado para condensar 2,73k g / s de vapor de água saturado a 340K . A condensação ocorre na superfície externa d
37 - Seja o Problema 11.36.(a) Para m ˙ f , A = m ˙ q , B =10k g / s , determine as temperaturas de saída do ar e da amônia, assim como a taxa de transferência de calor.(b) Represente graficamente as
40 -Vapor de água saturado a 0,14b a r é condensado em um trocador de calor casco e tubos com um passe no casco e dois passes nos tubos. O trocador tem 130 tubos de latão, cada um com um comprimento p
44 - Vapor de água saturado deixa uma turbina a vapor a uma vazão de 1,5k g / s e a uma pressão de 0,51b a r . O vapor deve ser completamente condensado em líquido saturado em um trocador de calor cas
49 - Um trocador de calor casco e tubos deve aquecer 10.000k g / h de água de 16 a 84 ℃ ℃, utilizando óleo de motor quente que escoa através do casco. O óleo faz um único passe no casco, entrando a 16