Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 133

Considere um trocador de calor água - água em contracorrente de com as seguintes especificações. A água quente entra em 90°C, enquanto a água fria entra em 20°C. A temperatura de saída da água quente é 15°C superior à da água fria, e a vazão mássica da água quente é 50% maior que a da água fria. O produto da superfície de transferência de calor e do coeficiente global de transferência de calor é 22 00 W K . Tomando o calor específico da água fria e quente em c p = 4180 J k g K , determine:

  1. A temperatura de saída da água fria;
  2. A eficácia do trocador de calor;
  3. A vazão mássica da água fria;
  4. A taxa de transferência de calor.

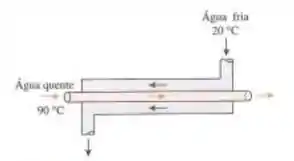
Passo 1

Bora continuaaar ...

Primeira coisa que precisamos fazer é achar a transfrencia de calor, ok?

Mas como?

Fácil!! Podemos usar a fórmula:

Q ˙ = m f ˙ c p T f ,   s a i - T f ,   e n t r a

E o que sabemos?

T f ,   e n t r a = 2 0 ° C

c p = 4 18 0 J k g K

Ainda não temos a vazão mássica nem a transferência de calor, então vamos ter que acha-los!

Começando pelo calor nós vamos usar a equação acima, só que para a água quente:

Q ˙ = m q ˙ c p T q ,   e n t r a - T q ,   s a i

Sabendo que:

m q ˙ = 1,5 m f ˙

c p , q = 4180 J k g K

T q ,   e n t r a = 90 ° C

T q ,   s a i = T f ,   s a i + 1 5 ° C

Substituindo:

Q ˙ = 1,5 m f ˙ 4180 J k g K 90 ° C - T f ,   s a i - 15 ° C

Q ˙ = 6270 m f ˙   75 - T f ,   s a i  

Q ˙ = ( 470250 - 6270 . T f ,   s a i ) m f ˙  

Com o calor nós podemos achar a temperatura de saída:

( 470250 - 6270 . T f ,   s a i ) m f ˙ = m f ˙ c p T f ,   s a i - T f ,   e n t r a

E substituindo nossos dados:

470250 - 6270 . T f ,   s a i = 4180 T f ,   s a i - 20

470250 - 6270 . T f ,   s a i = 4180 T f ,   s a i - 83600

553850 = 10450 . T f ,   s a i

T f ,   s a i = 53 ° C

É isso aí galera, achamos a primeira resposta !!

Bora pra segunda?

Passo 2

Para calcular a efetividade do trocador de calor podemos usar a equação:

ε = Q ˙ Q ˙ m a x

Vamos lembrar que:

Q m a x ˙ = C m i n T q ,   e n t r a - T f ,   e n t r a

E a taxa de transferência de calor real pode ser dada pela quantidade de calor recebida pelo ar:

Q ˙ = C f T f ,   s a i - T f ,   e n t r a

Para achar os valores de C nós precisamos lembrar que:

C = m ˙ c p

Então:

C q = m q ˙ c p

C f = m f ˙ c p

Vamos ver nossos dados?

c p = 4180 J k g K

m q ˙ = 1,5 m f ˙

Substituindo:

C q = 1,5 m f ˙ 4180 J k g K = 6270 m f ˙ W K

C f = m f ˙ 4180 J k g K = 4180 m f ˙   W K  

Agora sim nós vamos conseguir calcular o C mínimo e máximo, certo?

C m a x = C q = 6270 m f ˙ W K

C m i n = C f = 4180 m f ˙   W K

Então, na fórmula da efetividade:

ε = C f T f ,   s a i - T f ,   e n t r a C m i n T q ,   e n t r a - T f ,   e n t r a = T f ,   s a i - T f ,   e n t r a T q ,   e n t r a - T f ,   e n t r a

Lembrando que:

T f ,   e n t r a = 20 ° C

T f ,   s a i = 5 6 ° C

T q ,   e n t r a = 9 0 ° C

Substituindo:

ε = 5 6 ° C - 20 ° C 9 0 ° C - 20 ° C = 0,5 14

É isso aí !! Agora achamos a resposta da letra (b) !

Passo 3

Para calcular a vazão mássica nós podemos usar a fórmula do NTU:

N T U = U A s C m i n

Sabemos que:

U A s = 22 00 W K

C m i n = 4180 m f ˙   W K

Ainda não temos nada sobre o NTU, certo?

E para achar vamos usar a relação para o trocador de calor em contracorrente:

N T U = 1 C - 1 . ln ⁡ ε - 1 ε C - 1

Já sabemos que:

ε = 0,514

E:

C = C m i n C m a x

Substituindo:

C = 4180 m f ˙   W K 6270 m f ˙ W K = 0,667

Bora achar o NTU:

N T U = 1 0,667 - 1 . ln ⁡ 0,514 - 1 0,514 0,667 - 1

N T U = 0,906

Colocando tudo que sabemos na primeira fórmula:

0,906 = 22 00 W K 4180 m f ˙   W K

m f ˙ = 0,5809 k g s

Passo 4

Agora nós precisamos da letra (d), ou melhor, da taxa de transferência de calor!

Para isso vamos substituir na fórmula do passo 1 a vazão mássica que acabamos de achar:

Q ˙ = 0,5809 k g s 4180 J k g K 53 ° C - 20 ° C

Q ˙ = 80132,45   W

Ou melhor:

Q ˙ = 80 , 1   k W

Gostaram?!

Resposta

  1. T f ,   s a i = 53 ° C ;
  2. ε = 0,514 ;
  3. m f ˙ = 0,5809 k g s ;
  4. Q ˙ = 80,1   k W .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trocador de calor de tubos geminados, operando em contracorrente, como aquele ilustrado no Exercício 11.29, tem 5m de comprimento e é usado para aquecer ar para um processo de secagem. Os tubos são
Em um laticínio, leite a uma vazão de 250l i t r o s / h o r a e a uma temperatura do c o r p od av a c a de 38,6 ° C , deve ser refrigerado até uma temperatura segura para o armazenamento de 13 ° C o
Água quente para uma operação de lavagem industrial é produzida através da recuperação de calor dos gases de exaustão de uma fornalha. É utilizado um trocador de calor de escoamento cruzado, com os ga
Como parte de um grande projeto, foi dada a tarefa a um aluno de projetar um trocador de calor que atinja as seguintes especificações:Como em muitas situações do mundo real, o cliente não revelou, ou
Uma caldeira usada para gerar vapor de água saturado tem a forma de um trocador de calor com escoamentos cruzados e tubos sem aletas, com a água escoando no interior dos tubos e um gás a alta temperat