Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 108

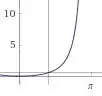
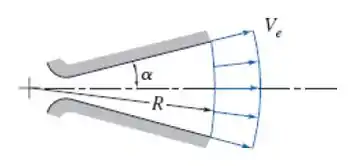
4.108 Os gases saindo do bocal de propulsão de um foguete são modelados como se escoassem radialmente para fora a apartir de um ponto a montante da garganta do bocal. Considere que a velocidade do escoamento na saída, V e , possui módulo constante. Desenvolva uma expressão para o empuxo axial, T a , resultante do escoamento deixando o plano de saída do bocal. Compare seus resultados com a aproximação unidimensional T = m ˙ V e . Avalie o erro percentual para α = 15 ° . Trace um gráfico do erro percentual v e r s u s   α para 0 ≤ α ≤ 22,5 ° .

Passo 1

O principal dessa questão e enchergarmos que a figura, na verdade, seria um círculo (imagina olhando de baixo pra cima, no ponto onde o escoamento é radial.

Vamos começar calculando o fluxo de massa:

m ˙ = ∫ 0 α ρ V e 2 π R   s e n   θ R   d θ

m ˙ = 2 π ρ V e R 2 - cos ⁡ θ 0 α

m ˙ = 2 π ρ V e R 2 1 - cos ⁡ α

Então a aproximação unidimensional que ele nos dá no enunciado fica:

T = 2 π ρ V e R 2 1 - cos ⁡ α V e

T = 2 π ρ V e 2 R 2 1 - cos ⁡ α

Passo 2

Agora vamos usar a equação da quantidade de movimento para achar T a .

T a = ∫ 0 α V e cos ⁡ θ ρ V e 2 π R   s e n   θ R   d θ

T a = 2 π R 2 ρ V e 2 ∫ 0 1 s e n   θ cos ⁡ θ   d θ

T a = π R 2 ρ V e 2   s e n 2 α

Passo 3

Para calcular o erro devemos lembrar que o erro percentural:

E R = T - T a T a

E R = 2 π ρ V e 2 R 2 1 - cos ⁡ α - π R 2 ρ V e 2   s e n 2 α π R 2 ρ V e 2   s e n 2 α  

E R = 2 1 - cos ⁡ α - s e n 2 α s e n 2 α

E R = 2 1 - cos ⁡ α s e n 2 α - 1

Para α = 15 ° = π 12 ,

E R = 0,0173 = 1,73 %

Resposta

T a = π R 2 ρ V e 2   s e n 2 α

E R = 2 1 - cos ⁡ α s e n 2 α - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.81 Um dispositivo de formação de jato é mostrado no diagrama. A água é fornecida a p=10 kPa (manométrica) através da abertura flageada da água 1900 mm². A água sai do dispsitivo em um jato livre, em
4.80 Suponha que a curva do Problema 4.39 seja um segmento de um canal largo no plano horizontal. A pressão na entrada é de 170 kPa (abs) e na saída, 130 kPa (abs). Determine a força requerida para ma
Encha um balão de brinquedo com ar e, em seguida, solte-o em um quarto. Observe como o balão se desloca bruscamente de um lado para outro no quarto. Explique o que causa esse fenômeno.
O cotovelo redutor de 90 ° do Exemplo 4.6 descarrega para a atmosfera. A Seção 2 está localizada 0,3m à direita da Seção 1. Estimar o momento exercido pelo flange no cotovelo.
Desprezando a resistência do ar, que velocidade atinge um foguete 5s após o seu lançamento vertical a partir do repouso, se a sua massa inicial é de 350k g , a taxa de queima é de 10k g / s e os gases