Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 170
Desprezando a resistência do ar, que velocidade atinge um foguete após o seu lançamento vertical a partir do repouso, se a sua massa inicial é de , a taxa de queima é de e os gases são expelidos à pressão atmosférica com velocidade de em relação ao foguete? Qual seria a velocidade máxima? Trace um gráfico da velocidade do foguete em função do tempo para os primeiros minutos de voo.
Passo 1
Considerações Iniciais:
- Escoamento em estado estacionário;
- Escoamento incompressível;
- Escoamento com velocidade constante;
- Escoamento uniforme.
- Força de resistência desprezível.
Passo 2
Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:
Como estamos analisando um sistema , temos:
Não há resistência, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Então:
Passo 3
Como e :
Assim:
Integrando:
Passo 4
Calculando a velocidade do foguete 5 após o lançamento.
;
;
;
.
Então:
Passo 5
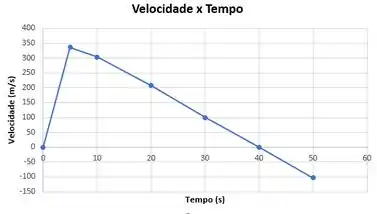
Traçando o gráfico da velocidade do foguete em função do tempo.
