Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 80

4.80 Suponha que a curva do Problema 4.39 seja um segmento de um canal largo no plano horizontal. A pressão na entrada é de 170 kPa (abs) e na saída, 130 kPa (abs). Determine a força requerida para manter a curva no lugar.

Passo 1

A curva do Problema 4.39 é:

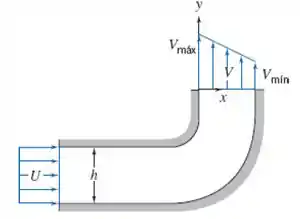
Vamos escolher um volume de controle que seja exatamente a nossa figura, ou seja, entra em A1 com velocidade U e sai em A2 com velocidade V.

Vamos começar pela equação de quantidade de movimento:

F → = F → R + F → B = ∂ ∂ t ∫ V C V → ρ   d V + ∫ S C V → ρ V → ⋅ d A →

Como o escoamento é em regime permanente,

∂ ∂ t ∫ V C V → ρ   d V = 0

Vamos desprezar o peso da curva e o peso da água dentro da curva, então:

F → B = 0

A componente x da equação de quantidade de movimento fica, então:

F → R x = ∫ A 1 U ρ V → ⋅ d A →

R x + p 1 A 1 = - ρ U 2 A 1

Atenção para esse sinal de menos que aparece porque U por causa do produto escalar entre V e dA.. é aquela parada do vetor velocidade estar em sentido oposto ao vetor normal à área... um blá blá blá, mas que faz diferença.

Como está meio confuso o enunciado, vamos considerar que a seção transversal seja quadrada, em outras palavras:

A 1 = h 2

Então:

R x = - p 1 h 2 - ρ U 2 h 2

R x = - h 2 p 1 + ρ U 2

Como h = 75,5   m m = 0,0755   m , U = 7,5   m / s e ρ = 999   k g / m 3 ,

Ahhhhhhhhhhh... como é dada a pressão absoluta, precisamos descontar a pressão atmosférias, então:

p 1 = 170 - 101

p 1 = 69   k P a

Substituindo:

R x = - 0,0755 2 69000 + 999 7,5 2

R x = - 714   N

Passo 2

A componente y da equação de quantidade de movimento fica, então:

F → R y = ∫ A 2 V ρ V → ⋅ d A →

R y - p 2 A 2 = ∫ ρ V 2 d x

Como V varia com x, então não podemos tirar da integral. Achando a equação que descreve V:

Em x = h ,   V = V m í n .

Considerando que varia linearmente, (fazendo certa mágica, mas é pensável pois é uma reta decrescente)

V = - A x + B

Em x = 0 , V = V m á x , do outro enunciado temos V m á x = 2   V m í n , então:

:

2   V m í n = - A 0 + B

B = 2 V m í n

Em x = h ,   V = V m í n :

V m í n = - A h + 2 V m í n

A = V m í n h

Ficamos, então com:

V = 2   V m í n - V m í n h x  

Substituindo,

R y - p 2 A 2 = ∫ 0 h   ρ 2   V m í n - V m í n h x   2 h d x

R y - p 2 A 2 = ∫ 0 h   ρ 4 V m í n 2 - 4 V m í n 2 h x + V m í n 2 h 2 x 2   2 h d x

R y - p 2 A 2 = ρ 4 V m í n 2 x - 2 V m í n 2 h x 2 + V m í n 2 h 2 x 3 3   h 0 h  

R y - p 2 A 2 =   ρ 4 V m í n 2 h - 2 V m í n 2 h h 2 + V m í n 2 h 2 h 3 3   h

R y = p 2 A 2 +   ρ 4 V m í n 2 h - 2 V m í n 2 h + V m í n 2 h 3   h

R y = p 2 A 2 +   ρ V m í n 2 h 2 4 h - 2 h + h 3  

Como A 2 = A 1 = h 2 ,

R y = p 2 h 2 +   ρ V m í n 2 h 2 4 h - 2 h + h 3  

R y = h 2 p 2 +   ρ V m í n 2 7 h 3  

Como h = 0,0755   m , ρ = 999   k g / m 3 , V m í n = 5   m / s (da outra questão) e p 2 = 130 - 101 = 29   k P a ,

R y = 0,0755 2 29000 + 999 5 2 7 0,0755 3

R y = 498   N

A força de resistência fica, então:

F r → = - 714 i ^ + 498 j ^ N

Resposta

F r → = - 714 i ^ + 498 j ^ N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.109 Quando um jato plano de líquido atinge uma placa inclinada, ele se parte em duas correntes de velocidades iguais, mas de espessuras desiguais. Para escoamento sem atrito, não pode haver força ta
4.106 Ar, na condição-padrão, escoa no longo de uma placa plana. A velocdiade da corrente livre, não perturbada, é U 0 = 20m / s . Em L = 0,4m a jusante da borda de ataque da placa, a espessura da cam
4.105 Um fluido com massa específica ρ = 750k g / m 3 escoa ao longo de uma placa plana de largura 1 m. A velocidade da corrente livre, não perturbada, é U 0 = 10m / s . Em L = 1m a jusante da borda d
4.104 Considere o escoamento incompressível de um fluido em uma camada-limite como descrito no Exemplo 4.2. Mostre que a força de arrasto devido ao atrito do fluido sobre a superfície é dada por F f =
4.108 Os gases saindo do bocal de propulsão de um foguete são modelados como se escoassem radialmente para fora a apartir de um ponto a montante da garganta do bocal. Considere que a velocidade do esc