Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 44

44. Considere a parede unidimensional mostrada na figura, que se encontra inicialmente a uma temperatura uniforme Ti e que é subitamente submetida à condição de contorno convectiva com um fluido a T∞.

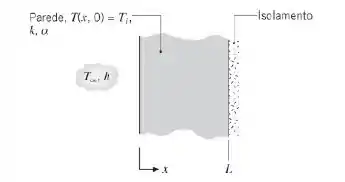
Para uma parede em particular, caso 1, a temperatura em x = L1, após t1 =100 s, é T1 = (L1, t1) = 315°C. Uma outra parede, caso 2, apresenta espessura e condições térmicas diferentes, conforme mostrado a seguir.

Quanto tempo será necessário para a segunda parede atingir 28,5°C na posição x = L2? Use como base para a sua análise a dependência funcional adimensional da distribuição de temperaturas transiente representada pela Equação 5.41.

Passo 1

De forma adimensional, a dependência funcional pode ser expressa como:

θ * = F ( x ' ,   F 0 ,   B i )

θ * = T x , t - T ∞ T i - T ∞

Para a parede 1:

B i 1 = 200 W m 2 . K 0,10 m 50 W m . K

B i 1 = 0,40

F 01 = 15 × 10 - 6 m 2 s ( 100 ) 0,10 2

F 01 = 0,150

θ 1 ' = 315 - 400 300 - 400

θ 1 ' = 0,85

Passo 2

Se os parâmetros x ' ,   B 0   ,   F 0 são iguais para ambas as paredes, então, θ 1 ' = θ 2 ' .

Para a parede 2:

B i 2 = 1 00 W m 2 . K 0,4 0 m 10 0 W m . K

B i 1 = 0,40

F 01 = 2 5 × 10 - 6 m 2 s ( t ) 0,4 0 2

F 01 = 1,562 × 10 - 4 t

θ 2 ' = 28,5 - 20 30 - 20

θ 2 ' = 0,85

Portanto,

F 01 = F 02

0,150 = 1,562 × 10 - 4 t

t 2 = 959,69   s

Portanto, o tempo necessário para a segunda parede atingir 28,5 C é, t 2 = 959,69   s .

Resposta

t 2 = 959,69   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera sólida de diâmetro igual a D = 100 m m , inicialmente a uma temperatura uniforme de T i = 50 ° C , é colocada em fluido escoando a uma temperatura de T ∞ = 20 ° C . As propriedades da esfer
Considere o duto bem isolado termicamente do Exemplo 5.4, que é subitamente sujeito ao escoamento de um óleo quente. Use uma rotina computacional para a condução transiente em paredes planas para obte
Seja o elemento combustível do Exemplo 5.9, que opera a uma taxa volumétrica de geração unifonne deq, — U)7 W/m3 , até que a taxa de geração mude subitamente para q2 = 2 x 107 W/m3 . Use uma rotina ge
A densidade e o calor específico de um material plástico são conhecidos (p = 950 kg/m3 , cp — 1100 J/(kg-K)), mas a sua condutividade térmica é desconhecida. Para determinar a condutividade térmica, é
Uma placa unidimensional com espessura 2L está inicialmente a uma temperatura uniforme 7). De repente, uma corrente elétrica é passada através da placa, causando um aquecimento volumétrico uniforme j(