Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 59

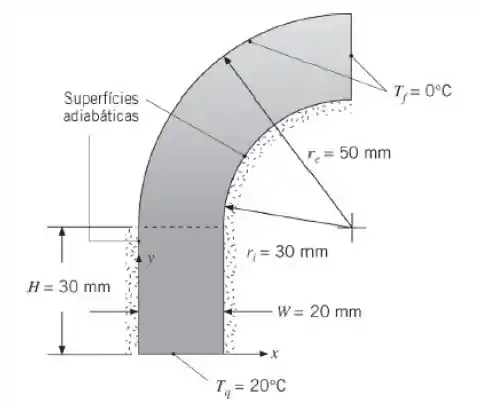
A condução no interior de geometrias relativamente complexas pode, às vezes, ser avaliada usando métodos de diferenças finitas deste livro, que podem ser aplicados em subdomínios e depois unidos. Considere o domínio bidimensional formado por um retângulo e um subdomínio cilíndrico unidos por uma superfície de controle comum, representada pela

linha tracejada. Note que, ao longo da superfície de contato, temperaturas nos dois subdomínios são idênticas e os fluxos condutivos locais para o subdomínio cilíndrico são idênticos aos fluxos condutivos locais saindo do subdomínio retangular. Calcule a taxa de transferência de calor por unidade de profundidade para dentro da página, q′, usando Δ x = Δ y = Δ r = 10   m m e Δ ϕ = π 8 . A base do subdomínio retangular é mantida a T q   =   20 ° C , enquanto a superfície vertical do subdomínio cilíndrico e a superfície do raio externo r e estão a T f = 0 ° C . As superfícies restantes são adiabáticas e a condutividade térmica é k   =   10 W m K .

Passo 1

Vamos para mais uma desenho, galerinha?

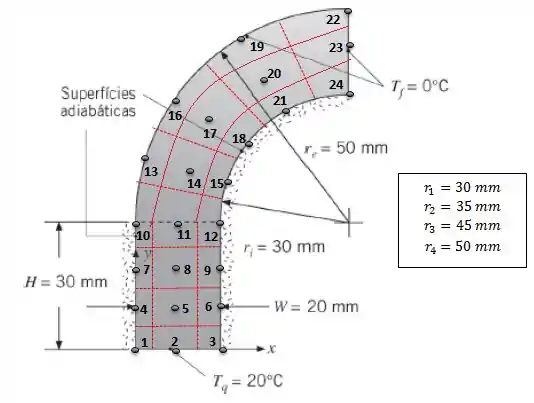
Vamos começar pela parte retangular, ok?

Pela Figura nós vemos que:

T 1 = T 2 = T 3 = 20 ° C

O Ponto 4 recebe calor por condução dos pontos 1, 5 e 7:

k ∆ x 2 T 1 - T 4 ∆ y + k ∆ x 2 T 7 - T 4 ∆ y + k ∆ y T 5 - T 4 ∆ x = 0

Como ∆ x = ∆ y :

20 + T 7 + 2 T 5 - 4 T 4 = 0                         ( i )  

O Ponto 5 recebe calor por condução dos pontos 2, 4, 6 e 8:

k ∆ x T 2 - T 5 ∆ y + k ∆ y T 6 - T 5 ∆ x + k ∆ x T 8 - T 5 ∆ y + k ∆ y T 4 - T 5 ∆ x = 0

20 + T 6 + T 8 + T 4 - 4 T 5 = 0                       ( i i )

O Ponto 6 recebe calor por condução dos pontos 3, 5 e 9:

k ∆ x 2 T 3 - T 6 ∆ y + k ∆ x 2 T 9 - T 6 ∆ y + k ∆ y T 5 - T 6 ∆ x = 0

20 + T 9 + T 5 - 4 T 6 = 0                         ( i i i )  

O Ponto 7 recebe calor por condução dos pontos 4, 8 e 10:

k ∆ x 2 T 4 - T 7 ∆ y + k ∆ x 2 T 10 - T 7 ∆ y + k ∆ y T 8 - T 7 ∆ x = 0

T 4 + T 10 + 2 T 8 - 4 T 7 = 0                         ( i v )  

O Ponto 8 recebe calor por condução dos pontos 5, 9, 11 e 7:

k ∆ x 2 T 5 - T 8 ∆ y + k ∆ y T 9 - T 8 ∆ x + k ∆ x T 11 - T 8 ∆ y + k ∆ y T 7 - T 8 ∆ x = 0

T 5 + 2 T 9 + 2 T 11 + 2 T 7 - 7 T 5 = 0                       ( v )

O Ponto 9 recebe calor por condução dos pontos 6, 8 e 12:

k ∆ x 2 T 6 - T 9 ∆ y + k ∆ y T 8 - T 9 ∆ x + k ∆ x 2 T 12 - T 9 ∆ y = 0

T 6 + T 8 + T 12 - 4 T 9 = 0                         ( v i )  

O Ponto 10 recebe calor por condução dos pontos 7 e 10, sem levar em consideração a parte cilíndrica.

E aqui nós temos o primeiro calor que deixa a parte retangular e vai para a cilíndrica, q ' 1 !

k ∆ x 2 T 7 - T 10 ∆ y + k ∆ y 2 T 11 - T 10 ∆ x = q ' 1

5 T 7 + 5 T 11 - 10 T 10 = q ' 1                         ( v i i )

O Ponto 11 recebe calor por condução dos pontos 8, 10 e 12, sem levar em consideração a parte cilíndrica.

E aqui nós temos o segundo calor que deixa a parte retangular e vai para a cilíndrica, q ' 2 !

k ∆ x T 8 - T 11 ∆ y + k ∆ y 2 T 10 - T 11 ∆ x + k ∆ y 2 T 12 - T 11 ∆ x = q ' 2

10 T 8 + 5 T 10 + 5 T 12 - 20 T 11 = q ' 2                         ( v i i i )

O Ponto 12 recebe calor por condução dos pontos 9 e 11, sem levar em consideração a parte cilíndrica.

E aqui nós temos o terceiro calor que deixa a parte retangular e vai para a cilíndrica, q ' 3 !

k ∆ x 2 T 9 - T 12 ∆ y + k ∆ y 2 T 11 - T 12 ∆ x = q ' 3

5 T 9 + 5 T 11 - 10 T 12 = q ' 3                         ( i x )

Passo 2

Agora que nós acabamos o retangular nós vamos olhar a parte cilíndrica !!

Olhando na figura nós obtemos que:

T 10 = T 13 = T 16 = T 19 = T 22 = T 23 = T 24 = 0 ° C

Para o Ponto 11 nós temos o calor que sai da parte retangular mais a análise normal, ok? Aqui temos que acrescentar a condução vindo dos pontos 10, 12 e 14:

k 3,5 ∆ r Δ ϕ 2 T 1 2 - T 11 ∆ r + k ∆ r T 14 - T 11 4 ∆ r Δ ϕ + k 4,5 ∆ r Δ ϕ 2 T 10 - T 11 ∆ r + q ' 2 = 0

Substituindo v i i i :

11 , 87 T 12 + 6,37 T 14 - 4 2,01 T 11 + 10 T 8 = 0                       ( x )

Para o Ponto 12 nós temos o calor que sai da parte retangular mais a análise normal, ok? Aqui temos que acrescentar a condução vindo dos pontos 11 e 15:

k 3,5 ∆ r Δ ϕ 2 T 11 - T 12 ∆ r + k ∆ r 2 T 15 - T 12 3 ∆ r Δ ϕ + q ' 3 = 0

Substituindo i x :

11,88 T 11 + 4,25 T 15 - 21,12 T 12 + 5 T 9 = 0                       ( x i )

Para o Ponto 14 nós temos condução vindo dos pontos 11, 15, 17 e 13:

k ∆ r T 11 - T 14 4 ∆ r Δ ϕ + k 3,5 ∆ r Δ ϕ T 15 - T 14 ∆ r + k ∆ r T 17 - T 14 4 ∆ r Δ ϕ + k 4,5 ∆ r Δ ϕ T 13 - T 14 ∆ r = 0

0,64 T 11 + 1,37 T 15 + 0,64 T 17 - 4,41 T 14 = 0                       ( x i i )

Para o Ponto 15 nós temos condução vindo dos pontos 12, 14 e 18:

k ∆ r 2 T 12 - T 15 3 ∆ r Δ ϕ + k 3,5 ∆ r Δ ϕ T 14 - T 15 ∆ r + k ∆ r 2 T 18 - T 15 3 ∆ r Δ ϕ = 0

0,42 T 12 + 1,37 T 14 + 0,42 T 18 - 2,44 T 15 = 0                       ( x i i i )

Para o Ponto 17 nós temos condução vindo dos pontos 14, 16, 18 e 21:

k ∆ r T 1 5 - T 1 7 4 ∆ r Δ ϕ + k 3,5 ∆ r Δ ϕ T 1 8 - T 17 ∆ r + k ∆ r T 20 - T 17 4 ∆ r Δ ϕ + k 4 , 5 ∆ r Δ ϕ T 1 6 - T 17 ∆ r = 0

0,64 T 15 + 1,37 T 18 + 0,64 T 20 - 4,41 T 17 = 0                       ( x i v )

Para o Ponto 18 nós temos condução vindo dos pontos 15, 17 e 21:

k ∆ r 2 T 1 5 - T 1 8 3 ∆ r Δ ϕ + k 3,5 ∆ r Δ ϕ T 1 7 - T 18 ∆ r + k ∆ r 2 T 2 1 - T 18 3 ∆ r Δ ϕ = 0

0,42 T 15 - 1,37 T 17 + 0,42 T 21 + 2,22 T 18 = 0                       ( x v )

Para o Ponto 20 nós temos condução vindo dos pontos 17, 21 e 23:

k ∆ r T 1 7 - T 20 4 ∆ r Δ ϕ + k 3,5 ∆ r Δ ϕ T 21 - T 20 ∆ r + k ∆ r T 2 2 - T 20 4 ∆ r Δ ϕ = 0

0,64 T 17 + 1,37 T 21 - 2,65 T 20 = 0                       ( x v i )

Para o Ponto 21 nós temos condução vindo dos pontos 18, 20 e 24:

k ∆ r 2 T 1 8 - T 21 3 ∆ r Δ ϕ + k 3,5 ∆ r Δ ϕ T 20 - T 21 ∆ r + k ∆ r 2 T 2 4 - T 21 3 ∆ r Δ ϕ = 0

0,42 T 1 8 - 1,37 T 20 + 2,22 T 21 = 0                       ( x v i i )

Passo 3

Agora nós vamos resolver todas essas equações simultaneamente:

Achando as temperaturas:

T 1 = T 2 = T 3 = 2 0 ° C

T 10 = T 13 = T 16 = T 19 = T 22 = T 23 = T 24 = 0 ° C

T 4 = 14,11 ° C

T 5 = 14,29 ° C

T 6 = 14,41 ° C

T 7 = 7,86 ° C

T 8 = 8,66 ° C

T 9 = 9,03 ° C

T 11 = 3,46 ° C

T 1 2 = 4,40 ° C

T 14 = 1,04 ° C

T 15 = 1,59 ° C

T 1 7 = 0,33 ° C

T 1 8 = 0,54 ° C

T 20 = 0,10 ° C

T 21 = 0,16 ° C

Agora que nós achamos as temperaturas nós podemos calcular o calor transferido por unidade de comprimento pode ser expressa como:

q ' = q ' 1 + q ' 2 + q ' 3

Substituindo:

q ' = 5 T 7 - 10 T 11 + 10 T 8 + 5 T 9 - 5 T 12

q ' = 114,5 W m

Ufaaa !! Essa foi bem puxada ein !!

Resposta

q ' = 114,5 W m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As temperaturas (°C), em regime estacionário, associadas a pontos nodais selecionados em um sistema bidimensional com uma condutividade térmica de 1,5 W m K , são mostradas na malha mostrada na figura
Seja uma longa barra com seção transversal quadrada (0,8 m de lado) e condutividade térmica de 2 W m K . Três laterais da barra são mantidas a uma temperatura uniforme de 300°C. A quarta superfície es
Uma análise por diferenças finitas, em condições de regime estacionário, foi efetuada em uma aleta cilíndrica com um diâmetro de 12 mm e condutividade térmica de 15 W m K . O processo de transferência
Considere uma aleta plana triangular, bidimensional, com comprimento L = 50 mm e espessura na base de t = 20 mm. A condutividade térmica da aleta é k=25 W m K . A temperatura de sua base é T b=50 ° C
Seja a condução bidimensional, em regime estacionário, em uma seção transversal quadrada com temperaturas superficiais especificadas. Determine as temperaturas nos nós 1, 2, 3 e 4. Estime a temperatur