Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 94
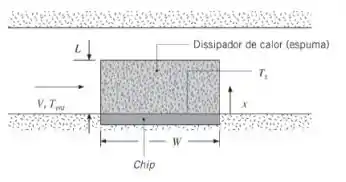
A espuma metálica do Problema 7.113 é soldada na superfície de um chip de silício de largura W = 25 mm. O dissipador na forma de espuma tem altura de L = 10 mm. Ar a uma temperatura de Tent = 27°C e com uma velocidade de V = 5 m/s atinge o dissipador de calor, enquanto a superfície do chip é mantida a 70°C. Determine a taxa de transferência de calor saindo do chip. Para fazer uma estimativa conservativa da taxa de transferência de calor, despreze a convecção e a radiação nas superfícies superior e laterais do dissipador de calor.
Passo 1
Esse exercício pede pra gente determinar a taxa de transferência de calor, e nos deu vários dados, mas mesmo assim precisamos de dados adicionais… E pra isso vamos lá no apêndice do livro, na tabela A-1, com :
E na tabela A-4, com :
Show! Para encontrar a taxa de transferência de calor vamos usar a equação:
Tá faltando encontrar essas coisinhas para achar a taxa, então vamos para as continhas!
Passo 2
Temos nossas temperaturas dadas no enunciado… Precisamos encontrar então o e o , vamos começar com o segundo:
Passo 3
Agora partiu encontrar a emissividade… Começar pelo número de Reynolds:
Agora podemos encontrar o :
Agora vamos encontrar nossa :
Vamos poder encontrar o nosso :
Passo 4
Vamos continuar encontrando os termos que precisaremos para chegar ao resultado final!
Vamos agora para o , considerando :
E pela equação 11.4, temos:
E podemos calcular o , que será:
E teremos:
Nossa resistência será então:
Passo 5
Agora sim, teremos nossa emissividade:
E finalmente, podemos achar a taxa de transferência de calor:
Uhull! Arrasamos!