Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 63

Um recuperador é um trocador de calor que aquece ar usado em um processo de combustão pela extração de energia dos produtos da combustão. Ele pode ser usado para aumentar a eficiência de uma turbina a gás através do aumento da temperatura do ar que entra no combustor.

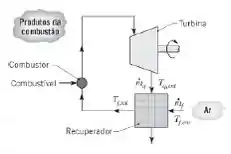
Seja um sistema no qual o recuperador é um trocador de calor de escoamento cruzado, com os dois fluidos não misturados, sendo as vazões associadas à exaustão da turbina e ao ar iguais a m ˙ q = 6,5   k g / s e m ˙ f = 6,2   k g / s , respectivamente. O valor correspondente do coeficiente global de transferência de calor é U = 100   W /   ( m 2 · K ) .

a) Sendo as temperaturas de entrada do gás e do ar T q , e n t = 700   K e T f , e n t = 300   K , respectivamente, qual área de transferência de calor é necessária para fornecer uma temperatura de saída do ar de T f , s a i = 500   K ? Tanto o ar quanto os produtos da combustão podem ser considerados com um calor específico de 1040   J /   ( k g · K ) .

Passo 1

Letra a)

Começamos o problema aplicando um balanço de energia:

q = q q = q f

q = C q T q , e n t - T q , s a i = C f T f , s a i - T f , e n t

Expandindo:

q = m ˙ q c p , q T q , e n t - T q , s a i = m ˙ f c p , f T f , s a i - T f , e n t

Calcularemos a capacidade térmica do fluído quente e do fluído frio:

C q = m ˙ q c p , q

C f = m ˙ f c p , f

Dados:

c p , q = c p , f = 1040   J / ( k g · K ) ;

m ˙ q = 6,5   k g / s ;

m ˙ f = 6,2   k g / s .

Temos:

C q = 6,5 ⋅ 1040

C q = 6760   W / K

C f = 6,2 ⋅ 1040

C f = 6448   W / K

Assim, temos que:

C m í n = C f

C m á x = C q

Passo 2

Agora, calcularemos a taxa de transferência de calor:

q = C f T f , s a i - T f , e n t

Sendo:

T f , s a i = 500   K ;

T f , e n t = 300   K .

Temos:

q = 6448 ⋅ 500 - 300

q = 1289,6   k W

A transferência de calor máxima se dá por:

q m á x = C m í n T q , e n t - T f , e n t

q m á x = C f T q , e n t - T f , e n t

Com:

T q , e n t = 700   K .

Temos:

q m á x = 6448 ⋅ 700 - 300

q m á x = 2579,2   k W

Passo 3

Agora, do seguinte modo, calculamos a eficácia do trocador de calor:

ε = q q m á x

ε = 1289,6 2579,2

ε = 0,5

E a razão das capacidades térmicas é dada por:

C r = C m í n C m á x = C f C q

C r = 6448 6760

C r = 0,964

Passo 4

Pela Figura 11.18, para um trocador de calor de fluxo cruzado com os dois fluidos não misturados, com ε = 0,5 e C r = 0,954 , obtemos:

N T U ≅ 1,10

Como o número de unidades de transferência ( N T U ) é dado por:

N T U = U A C m í n = U A C f

Com:

U = 100   W / ( m 2 · K ) .

Obtemos a área de transferência de calor:

1,10 = 100 ⋅ A 6448

A = 70,93   m 2

Resposta

A = 70,93   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A vazão mássica, calor específico e temperatura de entrada do lado do tubo de um trocador de calor de tubo duplo em escoamento paralelo são 3200 k g h , 2,0 k J k g K e 120°C, respectivamente. A vazão
A água geotérmica c p = 4250 J k g . K a 75°C deve ser utilizada para aquecer a água fresca c p = 4180 J k g . K a 17°C a uma taxa de 1,2 kg/s, em um trocador de calor de tubo duplo em contracorrente.
Vapor saturado de água condensa a 100°C no lado do casco de um trocador de calor de 1 passe no casco e dois 2 passes no tubo com área de superfície de 0,5 m² e um coeficiente global de transferência d
Ar a 18°C c p = 1006 J k g K deve ser aquecido a 58°C com óleo quente a 80°C c p = 2150 J k g K em um trocador de calor de escoamento cruzado com ar com mistura e óleo sem mistura. O produto da superf
Considere um trocador de calor de fluxo cruzado de único passe com ambos os fluidos não misturados. A água entra no tubo a 16°C e o deixa a 33°C, enquanto o óleo ( c p = 1,93 k J k g Keρ = 870 k g m 3