Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 82

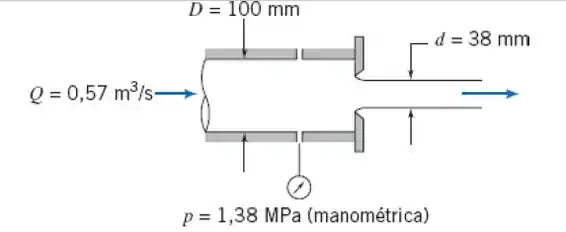
4.82 Uma placa plana com um orifício de 50 mm de diâmetro está instalada na extremidade de um tubo de 100 mm de diâmetro. Água escoa através do tubo e do orifício com uma vazão de 0,57 m³/s. O diâmetro do jato a jusante do orifício é 38 mm. Calcule a força externa necessária para manter a placa de orifício no lugar. Despreze o atrito na parede do tubo.

Passo 1

Vamos começar pela equação de quantidade de movimento:

F → = F → R + F → B = ∂ ∂ t ∫ V C V → ρ   d V + ∫ S C V → ρ V → ⋅ d A →

Como o escoamento é em regime permanente,

∂ ∂ t ∫ V C V → ρ   d V = 0

Vamos desprezar o peso do compartimento e o peso da água dentro do compartimento, então:

F → B = 0

A componente x da equação de quantidade de movimento fica, então:

F → R x = ∫ A 1 u ρ V → ⋅ d A →

R x + p 1 A 1 - p 2 A 2 = V 1 - ρ V 1 A 1 + V 2 ρ V 2 A 2

Atenção para esse sinal de menos que aparece por causa do produto escalar, blá blá blá. Em outras palavas, a normal à área está no sentido oposto, então fica negativo.

R x = - p 1 A 1 + p 2 A 2 + ρ V 2 2 A 2 - V 1 2 A 1

Passo 2

Da continuidade temos:

Q = V 1 A 1 = V 2 A 2

Podemos achar, então:

V 1 = Q A 1

V 2 = Q A 2

Considerando que a única pressão na saída é a pressão atmosférica, então p 2 = 0 .

R x = - p 1 A 1 + ρ Q A 2 2 A 2 - Q A 1 2 A 1

R x = - p 1 A 1 + ρ Q 2 A 2 - Q 2 A 1

Como a área da seção transversal é a área do disco,

R x = - p 1 π D 2 2 + ρ Q 2 π d 2 2 - Q 2 π D 2 2

Substituindo os valores:

R x = - 1380000 π 0,1 2 2 + ρ ( 0,57 ) 2 π 0,038 2 2 - 0,57 2 π 0,1 2 2

R x = 2,34 × 10 5   N

Resposta

R x = 2,34 × 10 5   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.93 Considere o escoamento permanente e adiabático de ar através de um longo tubo retilíneo com área de seçao transversal de 0,05 m². Na entrada do tubo, o ar está a 200 kPa (manométrica), 60°C e tem
4.98 Um bocal para um sistema de jateamento é projetado para produzir uma cortina de água radial e plana. A cortina de água sai do bocal com V 2 = 10m / s , cobre um arco de 180° e tem espessura t = 1
4.94 Uma caldeira monotubular consiste em um tubo de 6 m de comprimento de 9,5 mm de diâmetro interno. Água líquida entra no tubo a uma taxa de 0,135 kg/s com pressão de 3,45 MPa (abs). Vapor sai do t
4.95 Um gás escoa em regime permanente por meio de um tubo poroso aquecido, de área de seção transversal constante e igual a 0,15 m². Na entrada do tubo, a pressão absoluta é 400 kPa, a massa específi
4.100 A velocidade horizontal na esteira atrás de um objeto posicionado em uma corrente de ar de velocidade uniforme U é dada por u r = U 1 - cos 2 ⁡ π r 2 , r ≤ 1 u r = U , r1 Em que r é a coordenada