Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 95
4.95 Um gás escoa em regime permanente por meio de um tubo poroso aquecido, de área de seção transversal constante e igual a 0,15 m². Na entrada do tubo, a pressão absoluta é 400 kPa, a massa específica é 6 kg/m³ e a velocidade média é de 170 m/s. O fluido que atravessa a parede porosa sai em uma direção normal ao eixo do tubo com vazão mássica total de 20 kg/s. Na saída do tubo, a pressão absoluta é 300 kPa e a massa específica é 2,75 kg/m³. Determine a força axial do fluido sobre o tubo.
Passo 1
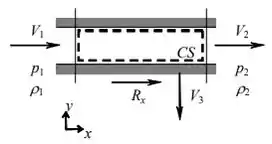
Usando a equação da continuidade podemos achar
Passo 2
Aplicando a equação da quantidade de movimento na componente x:
Resposta
Exercícios de Livros Relacionados
Um jato de água saindo de um bocal estacionário a 10m / s ( A j = 0,1m 2 ) atinge uma pá defletora montada sobre um carrinho conforme mostrado. A pá vira o jato em um ângulo θ = 40 ° . Determine o val
Um cilindro circular inserido através de uma corrente de água, conforme mostrado, deflete o escoamento de um ângulo θ . (Isto é chamado de “efeito Coanda”). Para a = 12,5m m , b = 2,5m m , V = 3m / s
Um tanque de água está apoiado dobre um carrinho com rodas sem atrito como mostrado. O carro está ligado a uma m = 10k g por meio de um cabo e coeficiente de atrito estático da massa com o solo é μ =
Uma placa vertical tem um orifício de bordas vivas no seu centro. Um jato de água com velocidade V atinge a placa concentricamente. Obtenha uma expressão para a força externa requerida para manter a p
Um trenó-foguete acelera do repouso sobre uma pista com resistências do ar e de rolamento desprezíveis. A massa inicial do trenó é m 0 = 600k g e o foguete contém inicialmente 150k g de combustível. O