Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 92

4.92 Um cotovelo redutor de 30° é mostrado. O fluido é água. Avalie as componentes da força que deve ser aplicada pelos tubos adjacentes para manter o cotovelo estático.

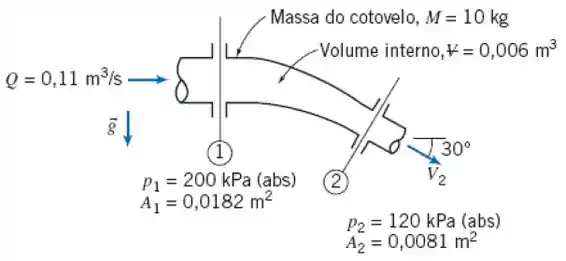
Passo 1

Vamos começar pelos dados que conseguimos tirar da vazão, ou seja, V 1 e V 2 .

Q = V 1 A 1 = V 2 A 2

V 1 = Q A 1

V 1 = 0,11 0,0182

V 1 = 6,04   m / s

V 2 = Q A 2

V 2 = 0,11 0,0081

V 2 = 13,58   m / s

Passo 2

Para a componente x da equação da quantidade de movimento:

R x + p 1 A 1 - p 2 A 2 cos ⁡ θ = V 1 - ρ V 1 A 1 + V 2 cos ⁡ θ ρ V 2 A 2

R x = - p 1 A 1 + p 2 A 2 cos ⁡ θ + V 1 - ρ V 1 A 1 + V 2 cos ⁡ θ ρ V 2 A 2

R x = - 200000 - 101000 0,0182 + 120000 - 101000 0,0081 3 2 + ( 6,04 ) - 999 6,04 0,0182 + 13,58 3 2 999 13,58 0,0081

R x = - 1040   N

Passo 3

Para a componente y da equação da quantidade de movimento:

R y - M g - ρ g V + p 2 A 2 s e n   θ = - V 2 s e n   θ ρ V 2 A 2

R y =   M g + ρ g V - p 2 A 2 s e n   θ - V 2 s e n   θ ρ V 2 A 2

R y = 10 9,81 + 999 9,81 0,006 - 120000 - 101000 0,0081 1 2 - 13,58 1 2 ( 999 13,58 0,0081

R y = - 666   N

Resposta

R x = - 1040   N

R y = - 666   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

For the water jet pump of Prob. P3.36, add the followingdata: p1 5 p2 5 25 lbf/in2, and the distance between sections 1 and 3 is 80 in. If the average wall shear stress between sections 1 and 3 is 7 l
Actual airflow past a parachute creates a variable distribution of velocities and directions. Let us model this as acircular air jet, of diameter half the parachute diameter,which is turned completely
For the boundary layer flow in Fig. 3.10, let the exit velocityprofile, at x 5 L, simulate turbulent flow, u (a) Find a relation between h and δ. (b) Find an expressionfor the drag force F on the plat
The Saturn V rocket in the chapter opener photo was powered by fi ve F-1 engines, each of which burned 3945 lbm/sof liquid oxygen and 1738 lbm of kerosene per second. Theexit velocity of burned gases
The horizontal nozzle in Fig. P3.49 has D1 5 12 in andD2 5 6 in, with inlet pressure p1 5 38 lbf/in2 absolute andV2 5 56 ft/s. For water at 208C, compute the horizontalforce provided by the fl ange bo