Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 80
Considere a mangueira e o bocal de incêndio do Problema 8.179. Especifique uma bomba e um diâmetro de rotor apropriados para alimentar quatro dessas mangueiras simultaneamente, Calcule a potência requerida pela bomba.
Passo 1
Beleza! Vamos começar o exercício aplicando o equilíbrio de energia para o sistema a saída da bomba (ponto 1) e a entrada do bocal (ponto 2):
Nesse caso, como o diâmetro da mangueira se mantém constante, e a vazão do sistema não muda, então temos e esses termos de velocidade se cancelam. Podemos desprezar também a diferença entre as cotas e , então a equação se torna:
E, sabemos que a perda de carga, contendo perdas distribuídas e localizadas, pode ser escrita como:
Nesse exercício, como o enunciado não mencionou, não temos perdas localizadas, então a equação para a perda de carga se torna:
Passo 2
Vamos pegar alguns dados do fluido da Tabela A.7 do livro:
Agora vamos substituir a expressão para a perda de carga na equação de energia, então, temos:
Chamando de , que corresponde a variação de pressão no sistema, que para esse trecho equivale à perda de carga nos 100 m de tubulação, e isolando , temos:
Tá legal, não temos o valor da velocidade e nem o valor do fator de atrito, que depende de , então vamos chutar um valor inicial de e iterar até ele convergir para o valor correto. Então, como o enunciado nos disse que a mangueira é lisa e feita de borracha, então iremos considerar a rugosidade superficial como:
Então, começando com um valor de e resolvendo para , temos:
Passo 3
Agora vamos calcular Reynolds para esse valor de velocidade:
Então agora podemos usar a equação de Colebrook e descobrir o valor do novo fator de atrito:
Substituindo os valores conhecidos (lembrando que só conseguimos resolver essa equação com o auxílio de uma calculadora), temos:
Agora vamos resolver novamente a equação para a velocidade, então, temos:
Passo 4
Agora vamos calcular Reynolds para esse valor de velocidade:
Então agora podemos usar a equação de Colebrook e descobrir o valor do novo fator de atrito:
Substituindo os valores conhecidos (lembrando que só conseguimos resolver essa equação com o auxílio de uma calculadora), temos:
Agora vamos resolver novamente a equação para a velocidade, então, temos:
Como esse valor de velocidade já está bem próximo do valor obtido no passo 3, vamos considerar que nosso valor já convergiu para o resultado esperado. Agora então podemos calcular a vazão para o sistema:
Passo 5
Agora vamos encontrar a carga da bomba, sabemos que ela é dada pela diferença de pressão entre a sua saída e entrada (lembrando que na saída da bomba devemos ter a mesma pressão que temos na entrada do bocal mais a parcela da perda de carga distribuída ao longo da tubulação), então, temos:
Substituindo os valores conhecidos, temos:
Então, para essa altura de carga e para a vazão encontrada no passo 4, podemos utilizar o diagrama de seleção de bombas a seguir:
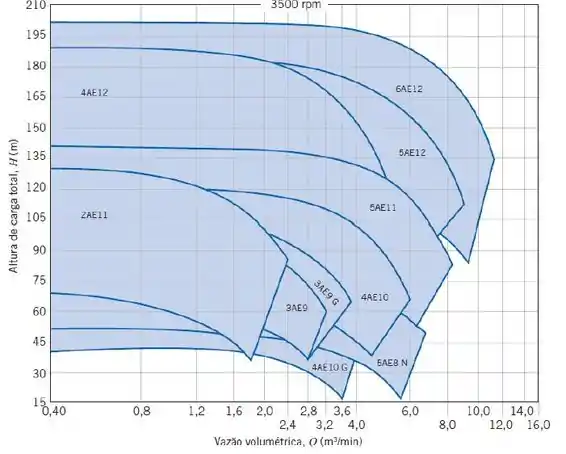
Então podemos escolher a bomba 2AE11 a 3500 rpm para esse caso.
Passo 6
Para estimar o diâmetro do rotor podemos utilizar o gráfico para a bomba 4AE12 a 3550 fornecido no livro:
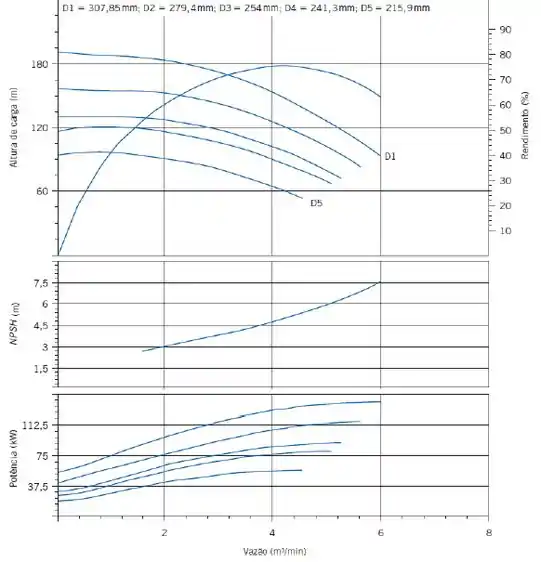
Então, para as condições de operação dadas, poderíamos pegar a curva do gráfico acima, assim teríamos:
Passo 7
Agora, para encontrar a potência requerida pela bomba, já que não temos um diagrama de eficiência específica para esse modelo, vamos assumir uma eficiência de 70% para realizar os cálculos, então, a potência requerida será:
No entanto, sabemos que a potência hidráulica é dada por:
Então, substituindo essa expressão na equação anterior, temos:
Substituindo os valores conhecidos, temos:
No entanto, essa é a potência para alimentar uma mangueira, para alimentar 4 mangueiras com essa vazão, iremos precisar de 4 vezes mais potência, então: