Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 142

Um carinho é propelido por um jato de líquido que sai horizontalmente de um tanque, conforme mostrado. A pista é horizontal e a resistência ao movimento pode ser desprezada. O tanque é pressurizado de modo que a velocidade do jato pode ser considerada constante. Obtenha uma expressão geral para a velocidade do carrinho à medida que ele acelera a partir do repouso. Se m 0 = 100   k g , ρ = 999   k g / m 3 e A = 0,005   m 2 , determine a velocidade do jato v requerida para que o carrinho atinja uma velocidade de 1,5   m / s após 30 segundos. Para esta condição, trace um gráfico da velocidade u como uma função do tempo. Trace um gráfico da velocidade do carrinho em função da velocidade do jato, para o tempo após 30 segundos.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = u ) ;
  4. Escoamento uniforme;
  5. Resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x - ∫ V C a r f x ρ d ∀ = ∂ ∂ t ∫ V C v ρ   d ∀ + ∫ S C v ( ρ V ) d A

Não há forças de campo atuando no sistema e nem resistência superficial, então, F B x = F S x = 0 :

- ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C v ρ   d ∀ + ∫ S C v ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

- ∫ V C a r f x ρ d ∀ = ∫ S C v ( ρ V ) d A

Sendo, V = u :

- ∫ V C a r f x ρ d ∀ = ∫ S C v 2 ρ d A

Integrando e analisando apenas o jato de saída, temos:

- a x ⋅ m = - v 2 ρ A

a x ⋅ m = v 2 ρ A

Passo 3

Temos que:

d m d t = - m ˙

d m = - m ˙   d t

∫ d m = - ∫ m ˙ d t

∫ m 0 m d m = - ∫ 0 t m ˙ d t

Integrando e aplicando os limites laterais:

m - m o = - m ˙ ⋅ t

m = m 0 - - m ˙ ⋅ t

Aplicando na equação obtida no Passo 2:

a x ⋅ m 0 - m ˙ ⋅ t = v 2 ρ A

Sendo d u d t = a x e m ˙ = ρ A V = ρ A v , temos:

d u d t m 0 - ρ A v ⋅ t = v 2 ρ A

Ajeitando a equação, obtemos:

d u = v 2 ρ A m 0 - ρ A v ⋅ t d t

∫ 0 u d u = ∫ 0 t v 2 ρ A m 0 - ρ A v ⋅ t d t

Integrando, obtemos a expressão geral para a velocidade do carrinho à medida que ele acelera a partir do repouso:

u = v ⋅ ln ⁡ m 0 m 0 - v ρ A t

Passo 4

A velocidade do jato v requerida para que o carrinho atinja uma velocidade de 1,5   m / s após 30 segundos é determinada por:

u = v ⋅ ln ⁡ m 0 m 0 - v ρ A t

Sendo:

u = 1,5   m / s ;

t = 30   s ;

m 0 = 100   k g ;

ρ = 999   k g / m 3 ;

A = 0,005   m 2 .

Temos:

1,5 = v ⋅ ln ⁡ 100 100 - 999 ⋅ 0,005 ⋅ 30 ⋅ v

Utilizando de programas matemáticos, obtemos que:

v = 0,610   m / s

Passo 5

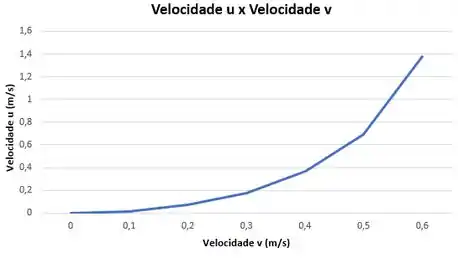
Com o auxílio do Excel, traçaremos um gráfico da velocidade do carrinho em função da velocidade do jato, que será obtida de 5 em 5 segundos.

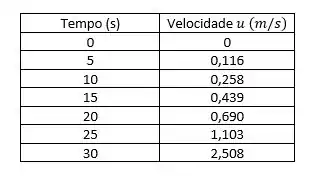
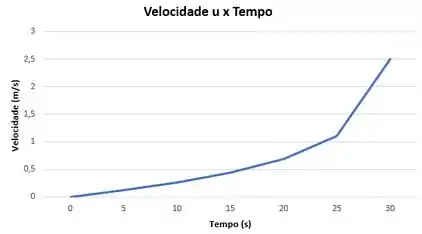
Passo 6

Com o auxílio do Excel, traçaremos um gráfico da velocidade do carrinho em função da velocidade do jato, sendo a velocidade v de 0 até 0,6   m / s que é aproximadamente o valor obtido com t = 30   s .

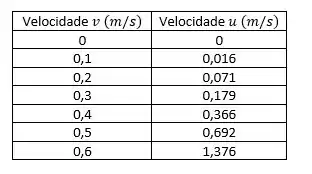
Resposta

u = v ⋅ ln ⁡ m 0 m 0 - v ρ A t

v = 0,610   m / s

Gráfico Velocidade u x Tempo

Gráfico Velocidade u x Velocidade v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fazendeiro compra 675k g de grãos, a granel, da cooperativa local. Os grãos são despejados na sua caminhonete através de um alimentador afunilado com um diâmetro de saída de 0,3m . O operador do al
Água escoa em regime permanente pelo bocal de uma mangueira de incêndio. A mangueira tem diâmetro interno de 75m m e a ponta do bocal de 25m m ; a pressão manométrica na mangueira é 510k P a e a corre
Um tipo de prato, raso e circular, tem um orifício de bordas vivas no centro. Um jato de água, de velocidade V , atinge o prato concentricamente. Obtenha uma expressão para a força externa necessária
Avalie o fluxo líquido de quantidade de movimento através do canal do Problema 4.38, se a profundidade normal ao diagrama for w = 1m .
Avalie o fluxo líquido de quantidade de movimento através do canal do Problema 4.39. Você esperaria que a pressão na saída fosse maior, menor ou a mesma que a pressão na entrada? Por quê?