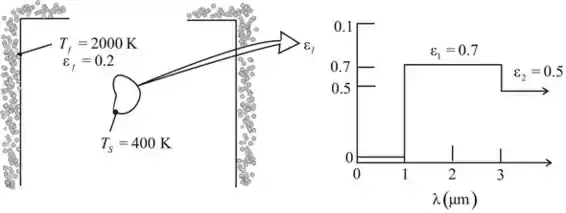
50 - Um pequeno objeto opaco e difuso, a , está suspenso em um grande forno cujas paredes internas estão a . As paredes são difusas e cinzas, e têm uma emissividade de . A emissividade hemisférica espectral da superfície do pequeno objeto é dada a seguir.

(a) Determine a emissividade total e a absortividade total da superfície.

(b) Avalie o fluxo radiante refletido e o fluxo radiante líquido para a superfície.

(c) Qual é o poder emissivo espectral em ?

(d) Qual é o comprimento de onda para o qual metade da radiação total emitida pela superfície se encontra na região espectral ?

a)

A emissividade hemisférica total da superfície é dada pela equação 12.38 como mostrado abaixo:

Como temos diferentes comprimentos de onda, envolvidas, podemos reescrever a equação acima da seguinte forma:

Pelo gráfico, podemos observar que: e .

Olhando o eixo vertical do gráfico, temos então,

A equação para a emissividade hemisférica total pode ser escrita em termos de fatores de emissão da banda, conforme mostrado a seguir:

Como sabemos os valores de , vamos substituir junto com os valores conhecidos para os intervalos de banda.

No enunciado foi dado que e . Logo:

Antes de continuarmos, precisaremos obter a fração da emissão total que é tabelada. Vamos consultar a Tabela 12.2, 'Funções de radiação do corpo negro' no valor de .

Aqui, é a fração da emissão total de corpos negros na banda espectral de para .

Para , teremos:

Voltando a equação da emissividade total, porém com todos os valores encontrados, podemos encontrá-la.

Vamos agora calcular a absortividade hemisférica total  que é dada pelas equações 12.45 e 12.46 como:

Assim como foi feito para a emissividade, podemos também fazer aqui, que é reescrever a equação acima em forma de fatores de emissão de banda, como mostrado a seguir:

Como o objeto é bem pequeno e é colocado em um grande forno, podemos considerar que

Portanto:

Logo:

Assim como feito na emissividade, precisaremos de novo de valores tabelas para diferentes combinações de temperatura e comprimento de onda, usando a tabela 12.1 agora.

Para e teremos:

Para , mantendo a temperatura, teremos:

Portanto, a absortividade hemisférica total é:

b)

Temos que o fluxo radiante refletido pode ser encontrada por meio da seguinte equação:

Onde , logo:

Temos também que a irradiação pode ser obtida como:

Portanto, ao juntarmos ambas equações, obtemos:

Já o fluxo radiante líquido para a superfície é dado por meio da relação:

Onde é a radiação emitida e é dada por:

Dessa forma o fluxo radiante líquido é:

c)

Temos e , logo:

Da tabela 12.1 temos:

Temos também que a emissividade pode ser dada como:

Como , temos:

d)

Para temos

Usando a tabela 12.2 temos que .