Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 57

57 - A absortividade hemisférica espectral de uma superfície opaca e a distribuição espectral da radiação que incide sobre a superfície estão mostradas na figura.

Qual é a absortividade hemisférica total da superfície? Se for considerado que ε λ = α λ e que a superfície está a 1000   K , qual é sua emissividade hemisférica total? Qual é o fluxo radiante líquido para a superfície?

Passo 1

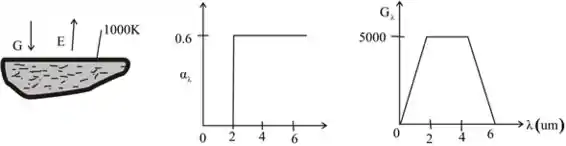
Passo 2

O fluxo radiante que é absorvido pela superfície pode ser calculado, já que temos no gráfico todas as variáveis. Vamos utilizar a integral utilizando o mesmo pensamento de dividir e 3 figuras o nosso desenho, dois triângulos e um retângulo.

G a b s = ∫ 0 ∞ α G λ d λ

= α 1 ∫ 0 2   μ m G λ d λ + α 2 ∫ 2   μ m 4   μ m G λ d λ + 1 2 α 3 ∫ 4   μ m 6   μ m G λ d λ

= 0 × 1 2 × 5000 × λ 0 2 + 0,6 × 5000 × λ 2 4 + 0,6 × 1 2 × 5000 × λ 4 6    

G a b s = 0 + 6000 + 3000

G a b s = 9000   W / m 2

Portanto, o fluxo radiante que é absorvido pela superfície é  9000   W / m 2 .

Passo 3

A irradiação total na superfície pode ser calculada por meio da integração da área em questão, entretanto, temos que a figura ao ser decomposta, torna-se um retângulo e dois triângulos, por isso, vamos dividir em três integrais, representando cada figura.

α = G a b s G

G = ∫ 0 ∞ G λ d λ

= 1 2 ∫ 0 2   μ m G λ d λ + ∫ 2   μ m 4   μ m G λ d λ + 1 2 ∫ 4   μ m 6   μ m G λ d λ

Repare que o termo 1 2 aparece, pois temos a área de um triângulo, que é dada pela área de um retângulo, dividido por 2 .

= 1 2 G λ ( 2 μ m - 0 μ m )   + G λ ( 4 μ m - 2 μ m ) + 1 2 G λ ( 6 μ m - 4   μ m )

= G λ + 2 G λ + G λ

Aqui, G λ é a irradiação no comprimento da onda λ .

G = 5000 + 10000 + 5000

G = 200 00   W / m 2

Portanto, a irradiação total na superfície é  20000   W / m 2 .

Passo 4

Precisamos agora, calcular a capacidade de absorção hemisférica total da superfície. Para isso iremos utilizar a relação entre os dois fluxos de energia presentes, já que essa absorção é uma fração da irradiação total que é absorvida.

α = G a b s G

= 9000 200 00

= 0 , 45

Portanto, a capacidade de absorção hemisférica total da superfície opaca é  0 , 45 .

Passo 5

A emissividade hemisférica total da superfície é dada pela equação 12.38 como mostrado abaixo:

ε T = ∫ 0 ∞ ε λ λ , T E λ , b λ , T d λ E b ( T )

Como temos diferentes comprimentos de onda, envolvidas, podemos reescrever a equação acima da seguinte forma:

ε T = ∫ 0 2 ε λ 1 E λ 1 , b d λ E b + ∫ 0 ∞ ε λ 2 E λ 2 , b d λ E b

A equação para a emissividade hemisférica total pode ser escrita em termos de fatores de emissão da banda, conforme mostrado a seguir:

ε T = ε λ 1 F ( 0 → 2 ) + ε λ 2 F ( 2 → ∞ )

Por meio do gráfico obtemos que:

ε 1 = 0 ; ε 2 = 0,6

Passo 6

No enunciado foi dado que T = 10 00   K e λ 1 = 2   μ m . Logo:

λ T = 20 00   μ m ⋅ K

Antes de continuarmos, precisaremos obter a fração da emissão total que é tabelada. Vamos consultar a Tabela 12.2, 'Funções de radiação do corpo negro' no valor de 2000   μ m ⋅ K .

λ T = 20 00   μ m ⋅ K

F 0 → 2 = 0 , 066728

Aqui, F 0 → 2 μ m   é a fração da emissão total de corpos negros na banda espectral de 0   para 2   μ m .

Passo 7

Voltando a equação de emissividade em termos de fatores de emissão da banda, temos:

ε T = ε λ 1 F ( 0 → 2 ) + ε λ 2 F ( 2 → ∞ )

= 0 + 0,6 [ 1 - F 0 → 2 ]

= 0 + 0,6 [ 1 - 0,066728 ]

ε = 0,5599

Passo 8

Já o fluxo radiante líquido para a superfície é dado por meio da relação:

α l i q = α G - E

Onde E é a radiação emitida e é dada por:

E = ε σ T s 4

Dessa forma o fluxo radiante líquido é:

α l i q = α 0,45 × 20000 - 0,5599 × 5,67 × 10 - 8 × 1000 4

= 90 00 - 32746,33

α l i q = - 22746,33   W / m 2

Resposta

G a b s = 9000   W / m 2

ε = 0,5599

α l i q = - 22746,33   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um forno com janela de vidro de 40 cm x 40 cm pode ser aproximado como um corpo negro a 1.200 K. Considerando que a transmissividade do vidro é 0,7 para radiação em comprimentos de onda inferiores a 3
Considere uma placa opaca horizontal bem isolada nas bordas e na superfície inferior. A placa é mantida a 500 K, tem absortividade hemisférica total de 0,51 e a seguinte função de emissividade espectr
Uma placa horizontal está passando por uma irradiação uniforme nas superfícies superior e inferior. A temperatura do ar ambiente em torno da placa é 290 K, com coeficiente de transferência de calor po
A variação da absortividade espectral de uma superfície é dada na figura a seguir. Determine a absortividade e a refletividade média da superfície para uma radiação originária de uma fonte a T = 2.500
Considere uma placa opaca horizontal bem isolada nas bordas e na superfície inferior. A placa é uniformemente irradiada de cima enquanto o ar a T ∞ = 300 K flui sobre a superfície, fornecendo um coefi