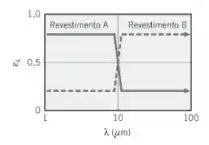
Um pequeno objeto metálico, inicialmente a Ti = 1000 K, é resfriado por radiação em uma câmara de vácuo a baixa temperatura. Uma das duas finas camadas de revestimento pode ser aplicada no objeto. As suas emissividades hemisféricas espectrais variam com o comprimento de onda como mostrado na figura. Com qual revestimento o objeto irá atingir mais rapidamente a temperatura de Tf = 500 K?

Temos uma questão interpretativa e teórica, certo? Vamos lá!

Bom, a emissividade hemisférica total pode ser obtida pela equação 12.43:

Vamos lembrar no momento em que , a emissividade muda de para . No caso do revestimento A, o tem o valor mais alto e o tem o valor mais baixo, já no caso do revestimento B, vamos ter o contrário, o tem o valor mais baixo e o tem o valor mais alto.

E pra gente encontrar o valor de , usando nosso , precisamos calcular:

Agora é só ir na tabela 12.2 e vemos que temos:

Então, nesse caso temos o revestimento A com a maior emissividade, que será acima de do espectro, certo?

Agora fazendo para , encontramos:

Indo na tabela 12.2 e temos:

E ainda assim o revestimento A vai ter o maior valor de emissividade, beleza?

Show de bola! Vemos que o revestimento A vai atingir o mais rapidamente!