Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 52

Considere uma superfície difusa e opaca com a absortividade espectral e a irradiação apresentadas a seguir:

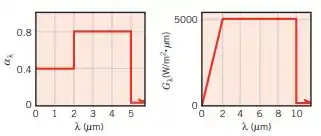
Qual é a absortividade total da superfície para a irradiação especificada? Se a superfície se encontra a uma temperatura de 500   K , qual é seu poder emissivo? Como a temperatura da superfície irá variar com o tempo, para as condições especificadas?

Passo 1

E aí, beleza?

Se ajeita aí e vem comigo resolver essa questão!

A primeira parte do nosso problema nos pede a absortividade total da superfície para a irradiação especificada, então:

α = G a b s G = ∫ 0 ∞ α λ G λ d λ   ∫ 0 ∞ G λ d λ  

Calculando a irradiação absorvida:

G a b s = 0,4 ⋅ 5000 ⋅ 2 2 + 0,8 ⋅ 5000 ⋅ 5 - 2 + 0 = 14000   W / m 2

Já a irradiação:

G = 2 ⋅ 5000 2 + 10 - 2 ⋅ 5000 = 45000   W / m 2

Desse modo:

α = 14000 45000

α = 0,311

Passo 2

A segunda parte nos pede o poder emissivo se a superfície se encontra a uma temperatura de 500   K :

ε = ∫ 0 ∞ ε λ E λ , b d λ E b = 0,4 ∫ 0 2 E λ , b d λ E b + ∫ 2 5 E λ , b d λ E b

Pela Tabela 12.2, obtemos:

λ T = 2 ⋅ 500 = 1000   μ m ⋅ K e F 0 → 2   μ m = 0,0003

λ T = 5 ⋅ 500 = 2500   μ m ⋅ K e F 0 → 5   μ m = 0 , 162

Assim:

ε = 0,4 ⋅ 0,0003 + 0,8 ⋅ 0,162 - 0,0003 = 0,13

Desse modo, o nosso poder emissivo se dá por:

E = ε E b = ε σ T 4 = 0,13 ⋅ 5,67 × 10 - 8 ⋅ 500 4

E = 460,7   W / m 2

Passo 3

Por fim, nos é pedido como a temperatura da superfície irá variar com o tempo, para as condições especificadas:

q ' ' = α G - E = 14000 - 460,7

q ' ' = 13539,3   W / m 2

Te espero na próxima questão!

Resposta

α = 0,311

E = 460,7   W / m 2

q ' ' = 13539,3   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma superfície difusa é caracterizada pela distribuição de emissividades hemisféricas espectrais mostrada na figura. Considerando temperaturas superficiais na faixa de 300 ≤ Ts ≤ 1000 K, em qual tempe
A janela de uma grande câmara de vácuo é fabricada com um material com características espectrais conhecidas. Um feixe colimado de energia radiante, gerado por um simulador solar, incide sobre a janel
A vigia (com 50 mm de diâmetro) de uma grande fornalha operando a 450°C é coberta com um material que tem τ = 0,8 e ρ = 0 para a irradiação originada no interior da fornalha. O material tem uma emissi
A emissividade direcional espectral de um material difuso a 2000 K apresenta a seguinte distribuição: Determine a emissividade hemisférica total a 2000 K. Determine o poder emissivo na faixa espectral
Considere uma superfície difusa e opaca cuja refletividade espectral varia em função do comprimento de onda conforme ilustrado. A superfície se encontra a 750K e a irradiação sobre um dos seus lados v