Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 36
5.36 Em um escoamento unidimensional e paralelo na direção positiva de , a velocidade varia lineramente de zero em até em . Determine uma expressão para a função de corrente, . Determine também a coordenada acima da qual a vazão volumétrica é a metade da total entre e .
Passo 1
Como é unidimensional e paralelo na direção positiva de , vamos ver a imagem que respresenta isso pra ficar mais fácil de entender o que ele quer dizer:
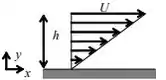
O campo de velocidade vai ter um cara tipo:
em ,
Passo 2
Usando a definição de função de corrente,
Separando as variáveis e integrando
Onde C é a constante de integração.
Passo 3
Para calcular a vazão volumétrica total:
Como ,
Para metade da vazão,
Como
Resposta
Exercícios de Livros Relacionados
No Exemplo 9–6, derivamos a equação para taxa de deformação volumétrica 1 V d V d t =∇ →.V → . Escreva isso como uma equação em palavra e discuta o que acontece com o volume de um elemento fluido à me
Repita o Exemplo 9–1 (gás comprimido em um cilindro por um pistão), mas sem usar a equação de continuidade. Em vez disso, considere a definição fundamental de densidade como massa dividida por volume.
Em muitas ocasiões, precisamos transformar uma velocidade de coordenadas cartesianas ( x ,y ,z ) em coordenadas cilíndricas ( r ,θ ,z ) (ou vice-versa). Usando a Fig. P9–13 como guia, transforme os co
Usando a Fig. P9–13 como guia, transforme os componentes cartesianos de velocidade ( u ,v ,w ) em componentes cilíndricos de velocidade ( u r ,u θ ,u z ) . (Dica: Como o componente z da velocidade per
Um campo de velocidade permanente, bidimensional, incompressível, possui componentes de velocidade cartesiana u = C y x 2 +y 2 e v = - C x x 2 +y 2 , onde C é uma constante. Transforme essas component