Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 16

Um campo de velocidade permanente, bidimensional, incompressível, possui componentes de velocidade cartesiana u = C y x 2 +   y 2 e v = - C x x 2 +   y 2 , onde C é uma constante. Transforme essas componentes cartesianas de velocidade em componentes cilíndricos de velocidade u r   e   u θ , simplificando o máximo possível. Você deve reconhecer esse fluxo. Que tipo de fluxo é esse?

Passo 1

Faaaaala galerinhaa!!

Animados para seguir?

Já estamos carecas de saber que:

u r = u . cos ⁡ θ + v sen ⁡ θ

u θ = - u . sen ⁡ θ + v . cos ⁡ θ

O problema nos disse que:

u = C y x 2 +   y 2

v = - C x x 2 +   y 2

Substituindo:

u r = C y x 2 +   y 2 . cos ⁡ θ + - C x x 2 +   y 2 sen ⁡ θ

u θ = - C y x 2 +   y 2 . sen ⁡ θ + - C x x 2 +   y 2 . cos ⁡ θ

Só que nós ainda temos coordenadas cartesianas aqui, e queremos coordenadas cilíndricas !!

Para remover estas coordenadas teremos que relembrar de três equações dadas ao longo do capítulo:

r 2 = x 2 + y 2

x = r . cos ⁡ θ  

y = r . sen ⁡ θ

Colocando nas equações:

u r = C r . sen ⁡ θ r 2 . cos ⁡ θ + - C r . cos ⁡ θ r 2 sen ⁡ θ

u r = C sen ⁡ θ . cos ⁡ θ r - C sen ⁡ θ . cos ⁡ θ r = 0

E para a próxima:

u θ = - C r . sen ⁡ θ r 2 + - C r . cos ⁡ θ r 2 . cos ⁡ θ

u θ = - C . sen 2 ⁡ θ r - C . cos 2 ⁡ θ r = - C r sen 2 ⁡ θ + cos 2 ⁡ θ

u θ = - C r

Sendo assim:

u r ,   u θ = 0 ,   - C r

Isso nos trás um escoamento em linha de vórtex, vamos ver a Figura:

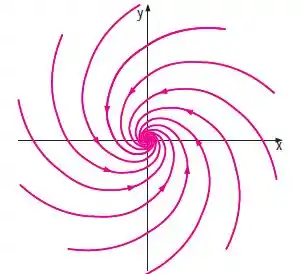
E é isso aí !!

Resposta

u r ,   u θ = 0 ,   - C r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja um meteorito que penetra na atmosfera. Admitir em primeira aproximação que o escoamento seja bidimensional e irrotacional na região próxima ao ponto de estagnação. Sabe-se que o escoamento pode s
Dado o campo de velocidades v → P , t = 6 x ⋅ e → x + 6 y ⋅ e → y + 7 t ⋅ e → z , determinarA velocidade e a aceleração no ponto ( 3 ; 2 ;z ) , no instante t = 1 As linhas de corrente no instante t =
A função de corrente de um escoamento plano de um fluido incompressível, entre duas placas infinitas, paralelas é dada por: Ψ = v 0 2 L y 2 Determinar o diagrama de velocidades e representa-lo grafica
As partículas de um fluido movem-se no plano x y com trajetórias definidas por x = x 0 + t ; y = y 0 + t 2 .Obter a equação e desenhar a trajetória da partícula que, no instante t=0, encontra-se em P
Dado o escoamento cujo campo de velocidades é: v x = x t ; v y = y t ; v z = 0 , determinarA equação da linha de corrente que passa pelo ponto P 1 2 ; 1 ; 2 A equação da trajetória que passa por P 1 ,