Usando a Fig. P9–13 como guia, transforme os componentes cartesianos de velocidade em componentes cilíndricos de velocidade . (Dica: Como o componente z da velocidade permanece o mesmo nessa transformação, precisamos apenas considerar o plano xy).

Bora seguir?

Então siiimboraaa..

Vamos colocar os ângulos que podemos observar na figura P9.14:

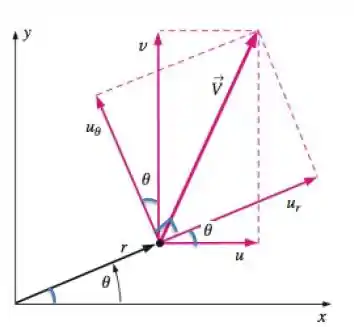
Agora que já achamos os ângulos nós podemos achar o em relação ao eixo x e ao eixo y.

Quando observamos na Figura nós podemos montar um triângulo em função de quando fazemos isso encontramos:

O que nos trás uma componente na direção x:

E na direção y:

Portanto, a componente é a soma destas duas, certo?

A mesma coisa para

E a componente

O valor da velocidade na direção z continua igual durante a transformação:

Sendo assim:

Basicamente o oposto do que vimos no exercício anterior, não é?

O mais difícil aqui é conseguir visualizar estas relações no desenho, percam um pouquinho de tempo na figura e depois vai ser sucesso !!