55 - Um pequeno disco com 5 mm de diâmetro está posicionado no centro de uma cúpula hemisférica isotérmica. O disco é difuso e cinza com uma emissividade de e é mantido a . A cúpula hemisférica, mantida a , tem um raio de e uma emissividade de .
Calcule a potência radiante deixando uma abertura de diâmetro igual a localizada na cúpula como mostrado.
Passo 1
A cúpula pode ser visualizada da seguinte maneira:
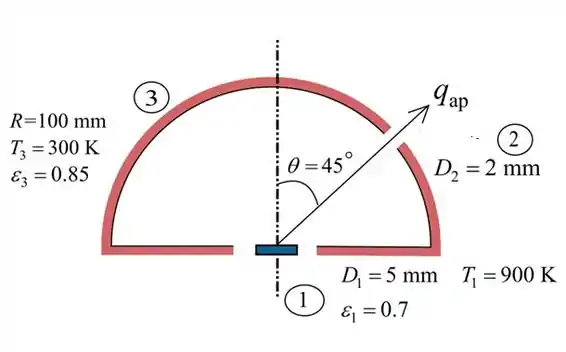
Onde é o disco, é abertura e é o revestimento.
Passo 2
A potência radiante que sai da abertura é igual à soma da radiação que sai do disco e da irradiação na abertura do gabinete e é dada pela seguinte relação.
Aqui, é a área da seção transversal da abertura (área normal ao fluxo de energia radiante), é a irradiação na abertura e é a radiação que sai do disco.
A radiação que sai do disco pode ser escrita em termos de radiocidade do disco da seguinte maneira:
Aqui, é a radiosidade do disco, é a área da seção transversal do disco, é o ângulo entre o normal e a linha que passa pela abertura e é o ângulo.
Passo 3
Podemos obter o ângulo sólido por meio da seguinte relação:
Aqui, é o raio do recinto hemisférico.
A radiosidade do disco pode ser expressa da seguinte maneira:
Aqui é a emissividade do disco, é a potência emissiva do gabinete preto, é a temperatura do disco, é a refletividade do disco, é a irradiação do disco e é a constante de Stephen Boltzmann.
Passo 4
A irradiação do disco e a irradiação na abertura do compartimento são iguais, o que pode ser expresso da seguinte forma:
Passo 5
Vamos comigo para encontrar a relação geral entre refletividade, absortividade e transmissividade do disco da seguinte maneira:
Aqui, a transmissividade é zero e, para a absorção e a emissividade do disco, é a mesma que o disco exibe um comportamento cinza.
Passo 6
Voltando a radiosidade do disco e fazendo as substituições pelos termos encontrados, passamos a ter:
Dessa forma a potência radiante que sai da abertura que é dada por:
Pode ser rescrita como:
Agora venha comigo para realizar as substituições e obter a potência desejada.
Portanto, a potência radiante que sai da abertura é .