Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 56

56 - A absortividade hemisférica espectral de uma superfície opaca tem o comportamento mostrado a seguir.

Qual é a absortividade solar, α S ? Se for considerado que ε λ = α λ e que a superfície se encontra a uma temperatura de 340   K , qual é sua emissividade hemisférica total?

Passo 1

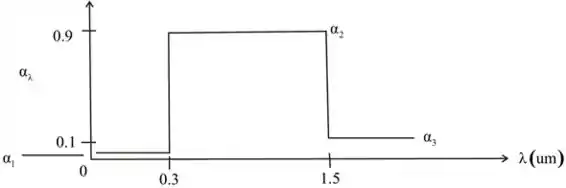
Passo 2

Temos que a temperatura de superfície é T = 340   K .

Temperatura do corpo é T = 5800 λ

Para encontrarmos a absorção total, podemos escrever sua equação por meio dos fatores da emissão da banda como:

α = α 1 F 0 → 0,3 + α 2 F 0,3 → 1,5 + α 3 F 1,5 → ∞

Que pode ser reescrita como:

α = α 1 F 0 → 0,3 + α 2 ( F 0 → 1,5 - F 0 → 0,3 ) + α 3 ( 1 - F 0 → 1,5 )

Antes de continuarmos, precisaremos obter a fração da emissão total que é tabelada. Vamos consultar a Tabela 12.2, 'Funções de radiação do corpo negro'.

Com λ = 0,3 e T = 5800   K , temos:

λ T = 0,3 × 5800   μ m ⋅ K

λ T = 8700   μ m ⋅ K

F 0 → 0 , 3 = 0 , 0335

Já com λ = 1,5 e T = 5800 logo:

λ T = 0,3 × 5800   μ m ⋅ K

λ T = 8700   μ m ⋅ K

F 0 → 0,3 = 0 , 8805

Voltando a equação da absorção, podemos finalmente obter seu valor.

α = α 1 F 0 → 0,3 + α 2 ( F 0 → 1,5 - F 0 → 0,3 ) + α 3 ( 1 - F 0 → 1,5 )

= 0 0,0335 + 0,9 0,8805 - 0,0335 + 0,1 ( 1 - 0,8805 )

α = 0,774

Passo 3

b) Agora venha comigo para encontrar a emissividade total:

Antes de continuarmos, precisaremos obter a fração da emissão total que é tabelada. Vamos consultar a Tabela 12.2, 'Funções de radiação do corpo negro'.

Com λ = 0 , 3 e T = 5800   K , temos:

λ T = 0,3 × 5800   μ m ⋅ K

λ T = 8700   μ m ⋅ K

F 0 → 1,5 = 0

Aqui, F 0 → 1 , 5   μ m   é a fração da emissão total de corpos negros na banda espectral de 0   para 1 , 5   μ m .

Portanto, temos que a emissividade é dada por:

ε = ε 1 F 0 → 1 , 5 + ε 2 F 1,5 → ∞

Que pode ser escrita como:

ε = ε 1 F 0 → 1 , 5 + ε 2 1 - F 0 → 1 , 5

Como temos todos os valores, basta substituir na equação acima e ser feliz!!!

ε = 0 + 0,1 ( 1 - 0 )

ε = 0,0 1

Portanto, a emissividade total é 0 , 01 .

Resposta

α = 0,774

ε = 0,01

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A transmissividade espectral de um vídeo regular de 3 mm de espessura pode ser expressa como τ 1 = 0 , p a r aλ0,35μ m τ 2 = 0,85 , p a r a0,35λ2,5μ m τ 3 = 0 , p a r aλ2,5μ m Determine a transmissivi
A transmissividade espectral de uma tampa de vidro utilizada em um coletor solar é dada por τ 1 = 0 , p a r aλ3μ m τ 2 = 0,85 p a r a0,3 ≤ λ ≤ 3μ m τ 3 = 0p a r aλ3μ m A radiação solar incide a uma ta
Fazendo referência à distribuição da transmissividade espectral do vidro com baixo teor de ferro (Figura 12.23 ), descreva sucintamente o que significa o “efeito estufa”. Isto é, como o vidro influenc
A transmissividade espectral de uma camada de água com 1m m de espessura pode ser aproximada como apresentada a seguir:(a) Água líquida somente pode existir abaixo da sua temperatura crítica, T c=647,
Radiação deixa um forno, que tem temperatura superficial interna de 1500K , através de uma abertura com 20m m de diâmetro. Uma porção dessa radiação é interceptada por um detector que se encontra a um