44 - Estime a emissividade hemisférica total ε de aço inoxidável polido a , usando a Equação 12.43 com as informações fornecidas na Figura 12.17. Suponha que a emissividade hemisférica é igual à emissividade normal. Efetue a integração usando um cálculo por bandas, dividindo a integral em cinco bandas, cada uma contendo 20% da emissão de um corpo negro a . Em cada banda, admita que a emissividade média esteja associada a um comprimento de onda mediano na banda , para o qual a metade da radiação do corpo negro no interior da banda esteja acima de (e metade esteja abaixo de ). Por exemplo, a primeira banda é de até , tal que e o comprimento de onda mediano para a primeira banda é achado de modo que. Também determine o poder emissivo da superfície.
Passo 1
A emissividade pode ser calculada usando a seguinte fórmula que está abaixo:
Aqui, a emissividade é .
Como cada banda possui 20% de emissão do corpo negro, vamos escolher o comprimento de onda médio para a primeira banda, de modo que .
Agora precisaremos obter um valor que por meio de valores tabelados conseguiremos. Vamos consultar a Tabela 12.2, 'Funções de radiação do corpo negro' onde temos a fração da emissão total que nos ajudara a encontrar o valor de por meio da interpolação em , como mostrado a seguir:
Passo 2
Agora podemos calcular o comprimento de onda médio, como mostrado abaixo.
Passo 3
Novamente precisamos de alguns valores tabelados, por isso, vamos consultar a Figura 12.17, 'Dependência espectral da emissividade espectral normal de materiais selecionados' para obter o valor da emissividade normal do aço inoxidável a polido no comprimento de onda de .
Passo 4
Vamos comigo, construir a tabela a seguir para todas as bandas seguindo os mesmos passos anteriores.
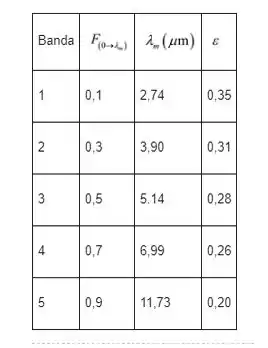
Passo 5
Na tabela acima, vamos calcular como mostrado abaixo:
Passo 6
Temos que a expressão para o poder emissivo é dada por:
Substituindo pelos valores conhecidos, passamos a ter:
Portanto, o poder emissivo da superfície é .