Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 61
A transmissividade espectral de uma camada de água com de espessura pode ser aproximada como apresentada a seguir:
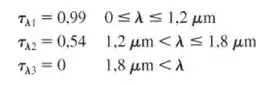
(a) Água líquida somente pode existir abaixo da sua temperatura crítica, . Determine a transmissividade total máxima possível de uma camada de de espessura de água líquida quando a água é guardada em um recipiente opaco e a ebulição não ocorre. Suponha que a irradiação seja a de um corpo negro.
(b) Determine a transmissividade de uma camada de de espessura de água líquida associada à fusão do fio de platina usado no experimento de ebulição de , como descrito na Seção .
(c) Determine a transmissividade total de uma camada de de espessura de água líquida exposta à irradiação solar. Suponha que o Sol emita como um corpo negro a .
Passo 1
Vamos lá, antes de mais nada vamos traçar o diagrama da transmissividade espectral para os parâmetros apresentados.
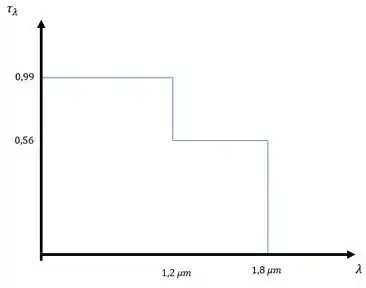
Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)
Da equação temos que a transmissividade global é dada por:
Onde:
Assim nossa transmissividade é:
Como :
Agora só aplicarmos as condições dadas.
Passo 2
(a)
Para uma temperatura de , temos:
Assim:
Passo 3
(b)
Para uma temperatura de , temos:
Assim:
Passo 4
(c)
Para uma temperatura de , temos:
Assim:
Curiosidade: A água pode ser considerada como opaca para a maioria das aplicações da engenharia, exceto para irradiação solar, temperaturas de irradiação extremamente altas como o plasma formado em processos de soldagem, que atingem temperatura na casa de , e para camadas muuuuuuuito finas de água.
Isso é tudo pessoal! \o/
