Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 68

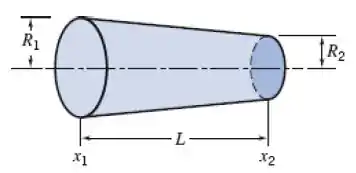
5.68 Considere o escoamento unidimensional e incompressível através do duto circular mostrado. A velocidade na seção 1 é dada por U = U 0 + U 1   s e n   ω t , em que U 0 = 20   m / s , U 1 = 2   m / s e ω = 0,3   r a d / s . As dimensões do duto são L = 1   m , R 1 = 0,2   m e R 2 = 0,1   m . Determine a aceleração da partícula na saída do duto. Trace um gráfico dos resultados como uma função do tempo para um ciclo completo. Sobre o mesmo gráfico, mostre a aceleração na saída do duto, se esse apresentar área constante em vez de convergente, e explique a diferença entre as curvas.

Passo 1

Com a equação da continuidade podemos achar a velocidade ao longo do duto.

V e A e = V A

U π R 1 2 = V π r 2

U 0 + U 1   s e n   ω t π R 1 2 = V π r 2

V = U 0 + U 1   s e n   ω t R 1 2 r 2

Mas podemos dizer que o raio varia linearmente com x, então (equação da reta):

r = a x + b

Quando x = x 1 = 0 , r = R 1 .

R 1 = a 0 + b

b = R 1

Quando x = x 2 = L ,   r = R 2 .

R 2 = a L + R 1

a = R 2 - R 1 L

Então:

r = R 2 - R 1 L x + R 1

A velocidade, em função de x, fica:

V = U 0 + U 1   s e n   ω t R 1 2 R 2 - R 1 L x + R 1 2

Passo 2

Como o escoamento é unidimensional (em x) e incompressível, podemos calcular a aceleração com:

a p x = V ∂ V ∂ x + ∂ V ∂ t

Vamos calcular as derivadas parciais:

∂ V ∂ x = - 2 R 2 - R 1 L U 0 + U 1   s e n   ω t R 1 2 R 2 - R 1 L x + R 1 3

∂ V ∂ t = ω U 1 R 1 2 cos ⁡ ω t R 2 - R 1 L x + R 1 2

Então:

a p x = U 0 + U 1   s e n   ω t R 1 2 R 2 - R 1 L x + R 1 2 - 2 R 2 - R 1 L U 0 + U 1   s e n   ω t R 1 2 R 2 - R 1 L x + R 1 3 + ω U 1 R 1 2 cos ⁡ ω t R 2 - R 1 L x + R 1 2

a p x = - 2 - 0,1 20 + 2   s e n   0,3 t 2 0,2 4 - 0,1 x + 0,2 5 + 0,3 2 0,2 2 cos ⁡ 0,3 t - 0,1 x + 0,2 2

a p x = - 2 - 0,1 20 + 2   s e n   0,3 t 2 0,2 4 - 0,1 x + 0,2 5 + 0,3 2 0,2 2 cos ⁡ 0,3 t - 0,1 x + 0,2 2

a p x = 0,00032 20 + 2   s e n   0,3 t 2 - 0,1 x + 0,2 5 + 0,024   cos ⁡ 0,3 t - 0,1 x + 0,2 2

Como é na saída do duto, então: x = x 2 = 1   m

a p x = 0,00032 20 + 2   s e n   0,3 t 2 - 0,1 1 + 0,2 5 + 0,024   cos ⁡ 0,3 t - 0,1 1 + 0,2 2

a p x = 0,00032 20 + 2   s e n   0,3 t 2 0,00001 + 0,024   cos ⁡ 0,3 t 0,01

a p x = 32 20 + 2   s e n   0,3 t 2 + 2,4   cos ⁡ 0,3 t

Passo 3

Se a área do duto fosse constante, ou seja, R 1 = R 2 ,

a p x = U 0 + U 1   s e n   ω t R 1 2 R 1 - R 1 L x + R 1 2 - 2 R 1 - R 1 L U 0 + U 1   s e n   ω t R 1 2 R 1 - R 1 L x + R 1 3 + ω U 1 R 1 2 cos ⁡ ω t R 1 - R 1 L x + R 1 2

a p x = U 0 + U 1   s e n   ω t R 1 2 0 L x + R 1 2 - 2 0 L U 0 + U 1   s e n   ω t R 1 2 0 L x + R 1 3 + ω U 1 R 1 2 cos ⁡ ω t 0 L x + R 1 2

a p x = U 0 + U 1   s e n   ω t R 1 2 R 1 2 0 + ω U 1 R 1 2 cos ⁡ ω t R 1 2

a p x = ω U 1 cos ⁡ ω t

Uma observação legal nesse ponto é que faz total sentido o nosso desenvolvimento porque conseguimos cortar os raios. Já que a área é constante, então a aceleração nao vai depender do raio.

a p x = 0,3 2 cos ⁡ ( 0,3 t )

a p x = 0,6 cos ⁡ ( 0,3 t )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.45 Considere o campo de velocidade no plano x y dado por V → = A x x 2 + y 2 i ^ + A y x 2 + y 2 j ^ , em que A = 10m 2 / s e x e y são medidos em metros. Este é um possível campo de escoamento inco
5.40 Considere o campo de escoamento dado por V → = a x 2 y i ^ - b y j ^ + c z 2 k ^ , em que a = 2m - 2 s - 1 , b = 2s - 1 e c = 1m - 1 s - 1 . Determine (a) o número de dimensões do escoamento, (b)
5.42 O campo de velocidade em uma camada-limite laminar é dado pela expressão V → = A U y x 1 2 i ^ + A U y 2 4 x 3 2 j ^ . Nesta expressão, A = 141m - 1 2 e U = 0,240m / s é a velocidade da corrente
5.57 Um campo de velocidade é representado pela expressão V → = A x - B i ^ - A y j ^ , em que A = 0,2s - 1 , B = 0,6ms - 1 e as coordenadas são medidas em metros. Obtenha uma expressão geral para a a
5.54 Um escoamento em onda de um fluido incompressível em uma superfície sólida segue um modelo senoidal. O escoamento é axissimétrico em torno do eixo z , o qual é normal à superfícies. A componente