Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 57
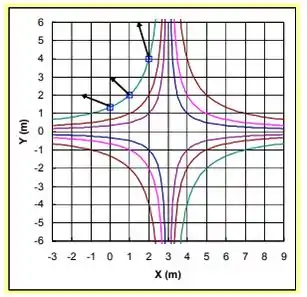
5.57 Um campo de velocidade é representado pela expressão , em que , e as coordenadas são medidas em metros. Obtenha uma expressão geral para a aceleração da partícula neste campo de velocidade. Calcule a aceleração das partículas fluidas nos pontos (0,4/3), (1,2) e (2,4). Trace algumas linhas de corrente no plano xy. Mostre os vetores de aceleração sobre o gráfico das linhas de corrente.
Passo 1
Para a aceleração da partícula
Como não depende de e admitimos regime permanente
Calculando as derivadas parciais
Como e
Passo 2
No ponto (0,4/3):
No ponto (1,2):
No ponto (2,4):
Passo 3
Pela definição de linhas de corrente
Separando as variáveis e integrando
Onde K é constante.
Manipulando matemáticamente
Vamos chamar
Resposta
Exercícios de Livros Relacionados
A componente x da velocidade em um campo de escoamento incompressível, bidimensional é dada por υ=- A x y , em que v é em m/s, as coordenadas são medidas em metros e A=1m - 1 s - 1 . Não há componente
Considere o escoamento do Problema 5.48. Avalie o módulo, direção e sentido da força resultante de pressão que age sobre aplaca superior entre ri e R, se ri = R/2.
Um campo de velocidade é dado por V → = A x 3 + B x y 2 i ^ + A y 3 + B x 2 y j ^ , A = 0,2m - 2 s - 1e B é uma constante e as coordenadas são medidas em metros. Determine o valor e as unidades de B c
Um líquido incompressível com viscosidade desprezível e massa específica ρ = 850 kg/m3 escoa em regime permanente através de um tubo horizontal. A área da seção transversal do tubo varia linearmente d
Um líquido incompressível com viscosidade desprezível e massa específica ρ = 1250 kg/m3 escoa em regime permanente através de um tubo de 5 m de comprimento com seção convergentedivergente, cuja área v