Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 81

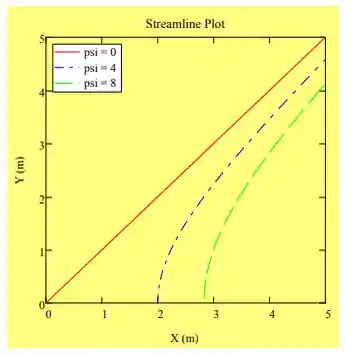
5.81 Um campo de escoamento é representado pela função de corrente ψ = x 2 - y 2 . Determine o campo de velocidade correspondente. Mostre que este campo de escoamento é irrotacional. Trace diversar linhas de corrente e ilustre o campo de velocidade.

Passo 1

Usando a definição de função de corrente:

u = ∂ ψ ∂ y

u = - 2 y

v = - ∂ ψ ∂ x

v = - 2 x

O campo de velocidade é, então:

V → = - 2 y i ^ - 2 x j ^

Passo 2

Em casos bidimensionais, para ser irrotacional

∂ u ∂ y - ∂ v ∂ x = 0

- 2 - - 2 = 0

0 = 0

Como satisfaz a equação, então é irrotacional.

Passo 3

Para traçar as linhas de corrente vamos manter ψ constante.

ψ = x 2 - y 2

y 2 = x 2 + ψ 2

y = ± x 2 + ψ 2

Resposta

V → = - 2 y i ^ - 2 x j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um detalhe sutil, muitas vezes esquecido pelos estudantes de mecânica dos fluidos (e até mesmo pelos seus professores!), é que uma região (potencial) de escoamento irrotacionalnão é a mesma coisa que
O que é o paradoxo de D'Alembert? Por que ele é um paradoxo?
Em uma região irrotacional do escoamento, o campo de velocidade pode ser calculado sem necessidade da equação do momento resolvendo a equação de Laplace para a função potencial de velocidade ϕ e depoi
Para cada afirmativa, decida se ela é verdadeira ou falsa e discuta a sua resposta brevemente. Essas afirmativas se referem à camada limite laminar sobre uma placa plana (Figura P 10 - 630 ).(a) Em um
Considere o seguinte campo de velocidade permanente, bidimensional, incompressível: V → = ( u , v ) = ( a x + b ) i → + ( - a y + c x ) j → . Esse campo de escoamento é irrotacional? Sefor, gere uma e