Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 82

5.82 Considere o campo de velocidade dado por V → = A x 2 i ^ + B x y j ^ , em que A = 3,3   m - 1 s - 1 , B = - 6,6   m - 1 s - 1 e as coordenadas são medidas em ft.

(a) Determine a rotação do fluido.

(b) Avalie a circulação sobre uma “curva” delimitada por y=0, x=0,3, y=0,3 e x=0.

(c) Obtenha uma expressão para a função de corrente.

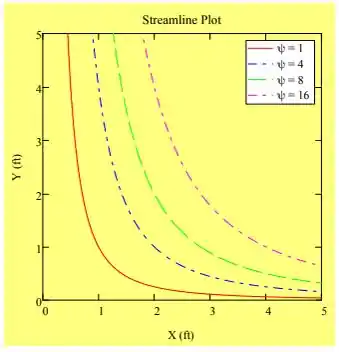
(d) trace diversa linhas de corrente no primeiro quadrante.

Passo 1

(a) Da definição de rotação:

ω → = 1 2 ∇ × V →

Como:

∇ = i ^ ∂ / ∂ x + j ^ ∂ / ∂ y + k ^ ∂ / ∂ z

E V → = A x 2 i ^ + B x y j ^ ,

ω → = 1 2 i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z A x 2 B x y 0

ω → = 1 2 B y k ^

Passo 2

(b) Da definição de circulação:

Γ = ∮ V → ⋅ d S

Graças ao bom deus podemos representar essa integral por: (por serem retas na vertical e na horizontal e bla bla bla)

Γ = ∫ x a x b u   d x + ∫ y b y c v   d y + ∫ x c x d u   d x + ∫ y d y a v   d x

Como u = A x 2 e v = B x y

Γ = ∫ a b A x 2   d x + ∫ b c B x y   d y + ∫ c d A x 2   d x + ∫ d a B x y   d x

Γ = A x 3 3 a b + B x y 2 2 b c + A x 3 3 c d + B x y 2 2 d a

Como os pontos são a = 0,0 , b = 1,0 , c = 1,1 e d = 0,1 ,

Γ = B 2

Γ = - 6,6 2

Γ = - 3,3   m - 1 s - 1

Passo 3

(c) Da definição de função de onda:

u = ∂ ψ ∂ y

A x 2 = ∂ ψ ∂ y

Vamos separar as variáveis e integrar em relação a y

d ψ = A x 2 d y

∫ d ψ = ∫ A x 2 d y

ψ = A x 2 y + C

Onde C é constante em relação a y.

Substituindo A = 3,3   m - 1 s - 1 , ficamos com

ψ = 3,3 x 2 y + C

Passo 4

Também da definiçã de função de onda:

v = - ∂ ψ ∂ x

B x y = - ∂ ψ ∂ x

Vamos separar as variáveis e integrar em relação a x

d ψ = - B x y   d x

∫ d ψ = ∫ - B x y   d x

ψ = - B x 2 y 2 + K

Onde K é constante em relação a x.

Substituindo B = - 6,6   m - 1 s - 1

ψ = - - 6,6 x 2 y 2 + K

ψ = 3,3 x 2 y + K

Comparando as duas funções de onda percebemos que C=K. Vamos tomar C=K=0 para simplificar, então:

ψ = 3,3 x 2 y

Passo 5

Para traçar as linhas de corrente é só tomar ψ como constante, então:

y = ψ 3,3 x 2

Resposta

(a) ω → = 1 2 B y k ^

(b) Γ = - 3,3   m - 1 s - 1

(c)

ψ = 3,3 x 2 y

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

17. A viscosidade do mel de trevo está listada em função da temperatura na Tabela P10-17. A gravidade específica do mel é aproximadamente 1,42 e não é uma função que dependa fortemente da temperatura.
10. Considere escoamento Poiseuille permanente, incompressível, laminar e totalmente desenvolvido entre duas placas paralelas horizontais ( os perfis de velocidade e pressão são mostrados na Figura P1
19. Estime a velocidade e o número de Reynolds do esperma mostrado na Figura 10-10. Esse microorganismo está nadando sob condições de escoamento lento? Suponha que ele está nadando em água à temperatu
12. No capitulo 9 (Exemplo 9-15), nós geramos uma solução ‘’exata’’ da equação de Navier-stokes para escoamento Couette totalmente desenvolvido entre duas placas planas horizontais (Figura P10-12), co
18. Para cada caso, calcule um número de Reynolds apropriado e indique se o escoamento pode ser aproximado pelas equações de escoamento lento. (a) Um microorganismo com diâmetro de 5,0 μ m nada na águ