Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 8.Problemas - Ex. 68

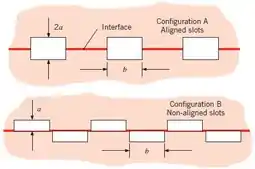
68 – Canais de fluxo retangulares são formados fresando fendas retangulares em placas planas de metal e soldando as placas juntas como mostrado abaixo. Canais grandes (Configuração A) ou duas vezes mais canais menores (Configuração B) podem ser formados mudando a posição relativa das placas para soldagem. Considere placas isotérmicas a TS=67°C com etileno glicol a Tm=27°C escoando a uma vazão de 0,1 kg/s em cada um dos canais grandes. A vazão em cada canal pequeno é 0,05 kg/s. Para dimensões a=10 mm e b=30 mm, determine a taxa de transferência de calor por unidade de comprimento do canal para um canal grande e para um par de canais pequenos. Também determine o gradiente de pressão no fluido associado com as configurações A e B.

Passo 1

Vamos começar equacionando a taxa de transferência de calor. Podemos usar a expressão da taxa de transferência de calor por convecção cuja expressão é

q c o n v = h A S ( T S - T m )

Onde,

-qconv é a taxa de transferência de calor por convecção;

-h é o coeficiente de transferência de calor;

-AS é a área superficial de troca térmica;

-TS é a temperatura da superfície;

-Tm é a temperatura da do fluido (etileno glicol);

Passo 2

Vamos agora mostrar quais são as áreas:

A área da superfície da placa maior é dada por

A S , m a i o r = 2 a b

E a área da superfície da placa menor é dada por

A S , m e n o r = a b

Assim, para a placa maior

q c o n v , m a i o r = h m a i o r 2 a b ( T S - T m )

A taxa por unidade de comprimento

q ' c o n v , m a i o r = 2 h m a i o r a ( T S - T m )

Para a placa menor

q c o n v , m e n o r = h m e n o r a b ( T S - T m )

A taxa por unidade de comprimento

q ' c o n v , m e n o r = h m e n o r a ( T S - T m )

Como deseja-se saber a taxa em um par de placas menores, então

q ' c o n v , m e n o r = 2 h m e n o r a ( T S - T m )

Passo 3

Os coeficientes de transferência de calor para a placa maior, hmaior, e para a placa menor, hmenor, são dadas pela expressão de Nusselt:

N u = h D h k

Onde,

-Dh é o diâmetro hidráulico;

-k é a condutividade térmica.

O diâmetro hidráulico é definido matematicamente como

D h = 4 A c P

Onde,

-Ac é a área de seção transversal;

-P é o perímetro molhado.

A c ,   m a i o r = 2 a b ; P m a i o r = 4 a + 2 b

A c ,   m e n o r = a b ;   P m e n o r = 2 a + 2 b

Assim,

D h , m a i o r = 8 a b 4 a + 2 b = 4 a b 2 a + b

D h , m a i o r = 4 ( 0,01   m ) ( 0,03   m ) 2 ( 0,01 m ) + 0,03 m = 0,024 m

D h , m e n o r = 4 a b 2 a + 2 b = 2 a b a + b

D h , m e n o r = 2 ( 0,01   m ) ( 0,03   m ) 0,01 m + 0,03 m = 0,015 m

Passo 4

Calculando Reynolds:

Dados da tabela para etino glicol, a T=300K:

k = 0,252 W m K ;   μ = 0,0157 k g m s ;   ρ = 1114,4 k g m 3

R e m a i o r = 4 m ˙ m a i o r π μ D h , m a i o r

R e m a i o r = 4 0,1 k g s π 0,0157 k g m . s 0,024 m = 338

R e m e n o r = 4 m ˙ m e n o r π μ D h , m e n o r

R e m e n o r = 4 0,05 k g s π 0,0157 k g m . s 0,015 m = 270,3

Passo 5

Com esses valores de Reynolds o escoamento é laminar para ambos os casos, assim para Nusselt, Nu, podemos usar o valor fixo de Nusselt para processo em escoamento laminar com temperatura da superfície constante, que é

N u = h D k = 3,66

Calculando os coeficientes de transferência de calor:

h m a i o r = 3,66 k D h , m a i o r

h m a i o r = 3,66 0,252 W m K 0,024 m = 38,43 W m 2 K

h m e n o r = 3,66 k D h , m e n o r

h m e n o r = 3,66 0,252 W m K 0,015 m = 61 , 5 W m 2 K

Passo 6

Calculando as taxas de transferência de calor por unidade de comprimento

Placa maior:

q ' c o n v , m a i o r = 2 38,43 W m 2 K ( 0,01 m ) ( 67 - 27 ) K

q ' c o n v , m a i o r = 30,7   W

Para a placa menor:

q ' c o n v , m e n o r = 2 61,5 W m 2 K ( 0,01 m ) ( 67 - 27 ) K

q ' c o n v , m e n o r = 49,2   W

Passo 7

A queda de pressão (gradiente de pressão) pode ser determinada pela eq. de Darcy-Weisbach:

∆ p = f 8 π 2 m ˙ 2 ρ D h 5 a

O fator de atrito para escoamento laminar é dado pela seguinte expressão:

f = 64 R e

Calculando as quedas de pressão:

∆ p m a i o r = 64 338 8 π 2 0,1 k g s 2 1114,4 k g m 3 0,024 m 5 ( 0,01   m )

∆ p m a i o r = 1,73   P a

∆ p m e n o r = 64 270,3 8 π 2 0,05 k g s 2 1114,4 k g m 3 0,015 m 5 ( 0,01   m )

∆ p m e n o r = 2,16   P a

Resposta

q ' c o n v , m a i o r = 30,7   W

∆ p m a i o r = 1,73   P a

q ' c o n v , m e n o r = 49,2   W

∆ p m e n o r = 2,16   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento aquecedor de 5m m de diâmetro é mantido com uma temperatura superficial de 350 ° C , quando imerso horizontalmente em água sob pressão atmosférica. A cobertura do elemento é de aço inoxidá
Um fluido dielétrico a pressão atmosférica é aquecido com um fio horizontal de platina com diâmetro de 0,5m m . Determine a temperatura do fio quando o fio é aquecido a 50 % do fluxo térmico crítico.
Tubos de cobre, com 25m m de diâmetro e 0,75m de comprimento, são usados para ferver água saturada a 1a t m . (a) Se os tubos operam a 75 % do fluxo térmico crítico, quantos tubos são necessários para
Considere uma caldeira que queima gás na qual cinco serpentinas de cobre, com parede delgada, diâmetro de 25m m e8m de comprimento, estão submersas em água pressurizada a 4,37b a r . As paredes das se
Um tubo de aço inoxidável (AISI 316 ), com parede espessa e diâmetros interno e externo de D i = 20m m e D e = 40m m , é aquecido eletricamente para fornecer uma taxa de geração térmica uniforme de q