Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 17

9.17 Avalie δ*/δ e θ/δ para o perfil de velocidade turbulento da lei de potência 1/7 dado no Problema 9.14. Compare com as razões para o perfil parabólico de velocidade de camada­limite laminar dado no Problema 9.10.

Passo 1

Para resolver esta questão, vamos usar estas duas relações:

δ 1 = ∫ 0 δ 1 - u U ⅆ y → D e f i n i ç ã o   d e   d e s l o c a m e n t o   d a   c a m a d a

θ = ∫ 0 δ u U 1 - u U ⅆ y → D e f i n i ç ã o   d e   M o m e t o   d a   C a m a d a

Passo 2

Vamos dividir em ambos por lados por δ e substituir dη = dy/δ:

δ ¹ δ   = ∫ 0 1 1 - u U d η

θ δ = ∫ 0 1 u U 1 - u U d η

Neste caso, a relação para a aproximação da curva 1/7 de potência, será usada a relação:

u U =   η 1 7

Substituindo em ambas equações teremos:

δ ¹ δ   = ∫ 0 1 1 - η 1 7 d η = 1 - 7 8 = 1 8 = 0,125

θ δ = ∫ 0 1 η 1 7 1 - η 1 7 d η = 7 8 - 7 9 = 0,0972

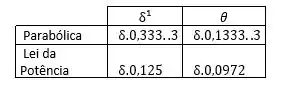
Os valores para a parábola foram calculados nos exercícios 8.15 e 8.16:

Para o perfil parabólico:

u U =   2 . η -   η 2

θ δ = ∫ 0 1 2 . η -   η 2 1 - 2 . η -   η 2 d η  

Resolvendo esta integral teremos:

θ δ =   1 - 5 3 + 1 - 1 5 = 0,1333 . . 3

Para o perfil parabólico define-se o deslocamento da camada como:

u U =   2 . η -   η 2

δ ¹ δ   = ∫ 0 1 1 - 2 . η -   η 2 d η  

Resolvendo esta integral teremos:

δ ¹ δ   =   1 - 1 + 1 3 = 0,333 . . 3

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um hidrofólio de 50 cm de comprimento e 4 m de largura move-se a 28 nós (1 nó = 1,852 kh/h) na água do mar a 20 °C. Aplicando a teoria da placa plana com R e t r = 5 E 5 , calcule seu arrasto, em N, (
Uma placa plana de comprimento L e altura δ é colocada em uma parede paralelamente a uma camada-limite que se aproxima, como na Figura P7.32. Admita que o escoamento sobre a placa seja totalmente turb
Uma análise alternativa do escoamento turbulento sobre uma placa foi feita por Prandtl em 1927, aplicando uma fórmula para a tensão cisalhante na parede do escoamento em um tubo τ p = 0,0225 ρ U 2 ν U
No escoamento de ar a 20°C e 1 atm sobre a placa plana da Figura P7.43, o cisalhamento na parede deve ser determinado na posição x por um elemento livre (de área pequena, conectado a um medidor de for
Considere o duto liso de seção quadrada de 10 cm por 10 cm na Figura P7.25. O fluido é ar a 20°C e 1 atm, escoando à V m é d i a = 24m / s é . Deseja-se aumentar a queda de pressão ao longo de 1 m de