Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 87

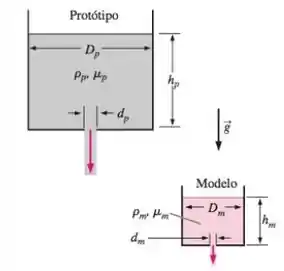
Um sistema de fornecimento de líquido está sendo criado de forma que o etileno glicol escoe por um orifício na parte inferior de um tanque grande, como mostra a Figura P7-87. Os projetistas precisam prever quanto tempo será necessário para que o etileno glicol seja completamente drenado. Como seria muito caro executar testes com um protótipo em escala real usando glicol, eles resolvem construir um modelo em escala 1 para 4 para os testes experimentais e pretendem água como seu líquido de teste. O modelo é geometricamente semelhante ao protótipo (Figura P8-87). (a) A temperatura do etileno glicol no tanque protótipo é de 60 °C, na qual ν = 4,75 × 10 - 6 m²/s. A que temperatura a água da experiência do modelo deve ser tomada para garantir a completa semelhança entre o modelo e o protótipo? (b) A experiência é feita com a água na temperatura adequada calculada na parte (a). São necessários 4,53 min para drenar o tanque modelo. Preveja o tempo que será necessário para drenar o etileno glicol do tanque protótipo.

Passo 1

Vamos começar escrevendo o tempo de drenagem em relação aos termos envolvidos no problema:

t d = f d , D , ρ , μ , h , g                 n = 7

Escrevendo esses parâmetros em termos das dimensões primárias, temos:

t d → t 1

d → L

D → L

h → L 1

ρ = m 1 L - 3

μ = m 1 L - 1 t - 1

g = L 1 t - 2

Vamos definir j = 3 , o número de dimensões primárias que estão representadas no problema. Assim, o número de grupos adimensionais Π é:

k = n - j = 7 - 3 = 4

Vamos escolher três parâmetros que se repetem, geralmente um parâmetro geométrico, um cinemático e um dinâmico

h ,   g   e   ρ

Com isso os números Π podem ser expressos como:

Π 1 = t d h a ρ b g c → Π 1 = t 1     L 1 a m 1 L - 3 b L 1 t - 2 c

Π 2 = d h d ρ e g f → Π 2 = { ( L 1 )   L 1 d m 1 L - 3 e L 1 t - 2 f

Π 3 = d h g ρ h g i → Π 2 = { ( L 1 )   L 1 g m 1 L - 3 h L 1 t - 2 i

Π 4 = μ h j ρ k g l → Π 2 = { ( m 1 L - 1 t - 1 )   L 1 j m 1 L - 3 k L 1 t - 2 l

Para o primeiro número Π temos:

Massa:

m 0 = m b → b = 0

Comprimento:

L 0 = L 1 L a L - 3 b L c → 0 = 1 + a - 3 b + c → a = - 1 - c

Tempo:

t 0 = t 1 t - 2 c → 0 = 1 - 2 c → c = 1 2

a = - 1 2

Assim:

Π 1 = t d h - 1 / 2 ρ 0 g 1 / 2 = t d g h    

Para Π 2 e Π 3 , temos números baseados no comprimento e assim temos:

Π 2 = d h

Π 3 = D h

Massa:

m 0 = m 1 m l → l = - 1

Comprimento:

L 0 = L 1 L j L - 3 k L l → 0 = 1 + j - 3 k + l → j = - 1 + 3 - l → j = 2 - k

Tempo:

t 0 = t - 1 t - 2 l → 0 = - 1 - 2 l → c = - 1 2

a = - 3 2

Logo:

Π 4 = μ h - 3 / 2 ρ - 1 g - 1 / 2 = μ ρ h 3 2 g

Ele pode ser modificado para “parecer” com a equação do número de Reynolds. Assim:

Π 4 = ρ h g h μ

Podemos escrever a relação entre os números Π como:

Π 1 = f Π 2 , Π 3 , Π 4 → t d g h   = f d h ,   D h ,   ρ h g h μ

Passo 2

Vamos analisar qual deve ser a temperatura da água no modelo para que a similaridade seja respeitada. Para isso vamos partir da relação obtida no passo 1. A similaridade é avaliada quando o número de Reynolds do modelo e do protótipo são iguais. Com isso, vamos comparar o termo semelhante ao número de Reynolds:

ρ h g h μ m = ρ h g h μ p → ρ m h m 3 2 g μ m = ρ p h p 3 2 g μ p

ρ m μ m = ρ p μ p h p h m 3 2

Como ν = μ / ρ , temos:

ν m = ν p h m h p 3 2

Para o etileno glicol a 60 °C, ν = 4,75 × 10 - 6 m²/s. Como h p / h m = 4 , podemos calcular a viscosidade do modelo:

ν m = 4,75 × 10 - 6 1 4 3 2 = 5,94 × 10 - 7   m 2 / s

Por interpolação das tabelas de propriedades, os projetistas devem realizar experimentos com água a uma temperatura de 45,8 °C.

Passo 3

Pode ser feita de forma semelhante ao passo 2 o cálculo do tempo de drenagem do tanque com etileno glicol. Fazendo:

t d g h   p = t d g h   m → t d p = t d m h p h m = 4,53 4 = 9,06   m i n

Resposta

  1. 45,8 °C
  2. 9,06 min
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A água a 20 °C escoa através de um tubo longo e reto. A queda de pressão é medida ao longo de uma seção do tubo de comprimento L = 1,3 m como uma função da velocidade média V no tubo (Tabela P7-70). O
Você precisará dos resultados do Problema 7-59 para resolver este problema. Uma minúscula partícula de aerossol cai com velocidade terminal constante V. O número de Reynolds ésuficientemente pequeno p
Combine os resultados dos Problemas 7-58 e 7-59 para gerar uma equação para a velocidade terminal V de um partícula de aerossol que cai no ar (Figura). Certifique-se de que o seu resultado é consisten
Repita o Problema 7-85, exceto por um parâmetro dependente diferente: o tempo necessário para esvaziar o tanque, t v a z i o . Gere uma relação adimensional para t v a z i o como função dos seguintes