Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 101
De acordo com um porta-voz da Pacific Gas & Eletric Company, a usina de Tiger Creek, localizada a leste de Jackson, na Califórnia, é uma das 71 usinas hidrelétricas da Companhia. A usina tem 373 m de altura de carga bruta, consome 21 m³/s de água, tem potência nominal de 60 MW e opera a 58 MW. Alega-se que a turbina produz 0,785 kW.h(m².m) de água e de operação. Estime a altura de carga líquida do local, a velocidade específica da turbina e a sua eficiência. Comente quanto à consistência interna desses dados.
Passo 1
Tá legal! A primeira coisa que devemos fazer nesse exercício é consultar a figura 10.37 apresentada nessa seção que relaciona a eficiência com a produção em porcentagem da carga total:
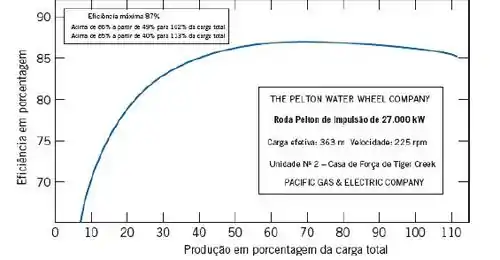
Vamos assumir que nesse caso temos a eficiência máxima, que de acordo com o gráfico, é de:
Então, com isso, conseguimos encontrar a carga líquida a partir da equação da potência produzida, que é dada por:
Substituindo os valores conhecidos, temos:
Então, para checar se o nosso palpite na eficiência é razoável, vamos dividir a carga líquida encontrada pela carga bruta disponível fornecida no enunciado, então, temos:
Então, podemos considerar a eficiência de .
Passo 2
Agora vamos analisar o gráfico que apresenta a eficiência em função da velocidade específica adimensional:
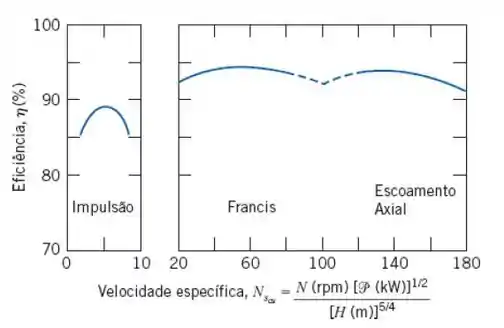
Desse gráfico, para uma turbina de impulsão e com , temos:
No entanto, conforme vimos nessa seção, essa velocidade específica é para o sistema de unidades típicas dos estados unidos, só que, nós já vimos no exercício 100 que para converter essa velocidade específica para aquela do sistem internacional, basta dividir esse valor por 43,5, então, temos:
E, a equação para a velocidade específica em unidades do sistema internacional é:
Então, substituindo os valores conhecidos, temos:
Convertendo esse valor para rpm, temos:
Passo 3
Agora para verificar os dados fornecidos, vamos primeiro converter a energia gerada para :
O valor fornecido no enunciado foi de , então, o valor que encontramos está até maior do que o fornecido. Agora vamos checar a produção por vazão de água em , então, temos:
E, convertendo esse valor para as unidades de interesse, temos:
O valor fornecido no enunciado foi de , chegamos bem perto, então o valor parece estar correto.